Ground State Masses of Nuclei
with a Probabilistic Neural Network


LA-UR-22-24945
Matthew Mumpower
Nuclear Data Working Group
Monday July 11$^{th}$ 2022

Theoretical Division
ML/AI: Text → image

A small cactus wearing a straw hat and neon sunglasses in the Sahara desert.
ML/AI: Text → bling

A bucket bag made of blue suede. The bag is decorated with intricate golden paisley patterns. The handle of the bag is made of rubies and pearls.
ML/AI: person generation

Every refresh of this page generates a new person (who does not exist)
Nuclear physics from a forward problem perspective

When we model nuclear properties we think of it as a 'forward' problem
We start with our model and parameters and try to match measurements / observations
This is an extremely successful approach and is generally how we use theory models
Mathematically: $f(\vec{\boldsymbol{x}}) = \vec{\boldsymbol{y}}$
Where $f$ is our model, $\vec{\boldsymbol{x}}$ are the parameters for the model and $\vec{\boldsymbol{y}}$ are the predictions
Forward problem... problems...

There can be many challenges with this approach
For instance: model computationally expensive or how do we update our model if we don't match data?
Or perhaps...
We don't always know what modifications are required or the physics could be very hard if not impossible to model given current computational limitations (e.g. many-body problem)
Treating this as an 'inverse problem' provides an alternative approach...
Nuclear physics from an inverse problem perspective

Suppose we start with the nuclear data (and its associated uncertainties)
We can then try to figure out what models may match relevant observations
This approach allows us to vary and optimize the model!
Mathematically, still: $f(\vec{\boldsymbol{x}}) = \vec{\boldsymbol{y}}$; but we want to now find $f$; fixing $\vec{\boldsymbol{x}}$
Machine learning and artificial intelligence algorithms are ideal for this class of problems...
How do we find $f$? An example...


My son Zachary has been very keen on learning his letters from an early age
Letters are well known (this represents the data we want to match to)
But the model (being able to draw - eventually letters) must be developed, practiced and finally optimized
This is a complex, iterative process - it takes times to find '$f$'!
Finding $f$... a first attempt

Example from 1 years old; random drawing episode; time taken: 10 minutes
Finding $f$... okay for real this time

Example from 2.5 years old; first ever attempt to draw letters / alphabet; time taken: 2 hours!
Finding $f$... now we're getting somewhere

Example from 3.5 years old; drawing scenery; time taken: 10 minutes
Finding $f$... something legible!

Example from 4 years old; tracing the days of the week; time taken: 30 minutes
Let's apply this idea to a basic property...
A relatively easy choice is a scalar property; how about atomic binding energies (masses)?
But... writing down the many-body quantum mechanical Hamlitonian is hard; want to find ground state
Recall: $f(\vec{\boldsymbol{x}}) = \vec{\boldsymbol{y}}$
$f$ will be a neural network (a model that can change)
$\vec{\boldsymbol{y}_{obs}}$ are the observations (e.g. Atomic Mass Evaluation) we want to match $\vec{\boldsymbol{y}}$ with
But what about $\vec{\boldsymbol{x}}$?
Why not a physically motivated feature space!?
proton number ($Z$), neutron number, ($N$), nucleon number ($A$), etc.
Network feature spaces ($\vec{\boldsymbol{x}}$)

We use a variety of possible physically motivated features as inputs into the model
Mixture Density Network
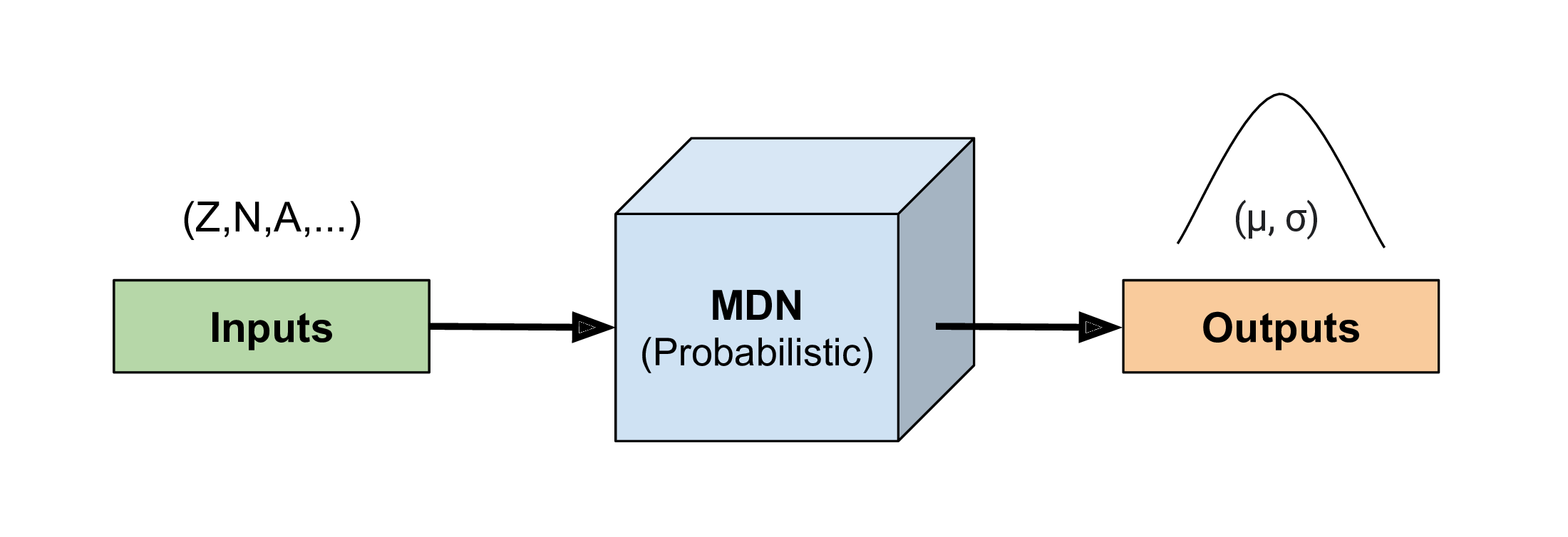
We take a Bayesian approach: our network inputs are sampled based on nuclear data uncertainties
Our network outputs are therefore statistical
We can represent outputs by a collection of Gaussians (for masses we only need 1)
Our network also provides a well-quanitfied estimate of uncertainty (fully propagated through the model)
Network topology: fully connected $\sim$4-8 layers; 8 nodes; regularization via weight-decay
Last layer converts output to Gaussian ad-mixture
Results: modeling atomic masses
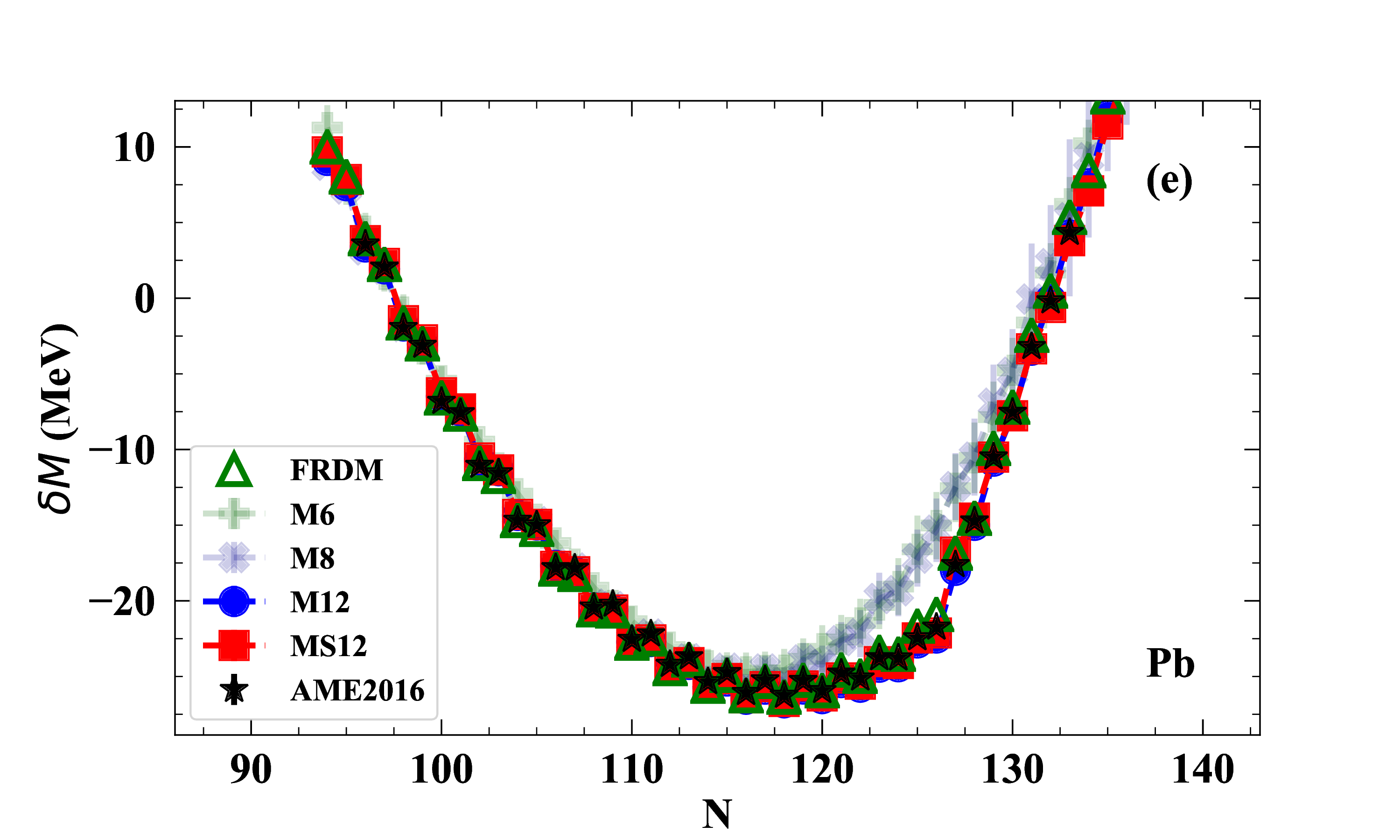
Here we show results along the lead (Pb) [$Z=82$] isotopic chain
Data from the Atomic Mass Evaluation (AME2016) in black stars
Increasing sophistication of the model feature space indicated by M##
Results: modeling atomic masses
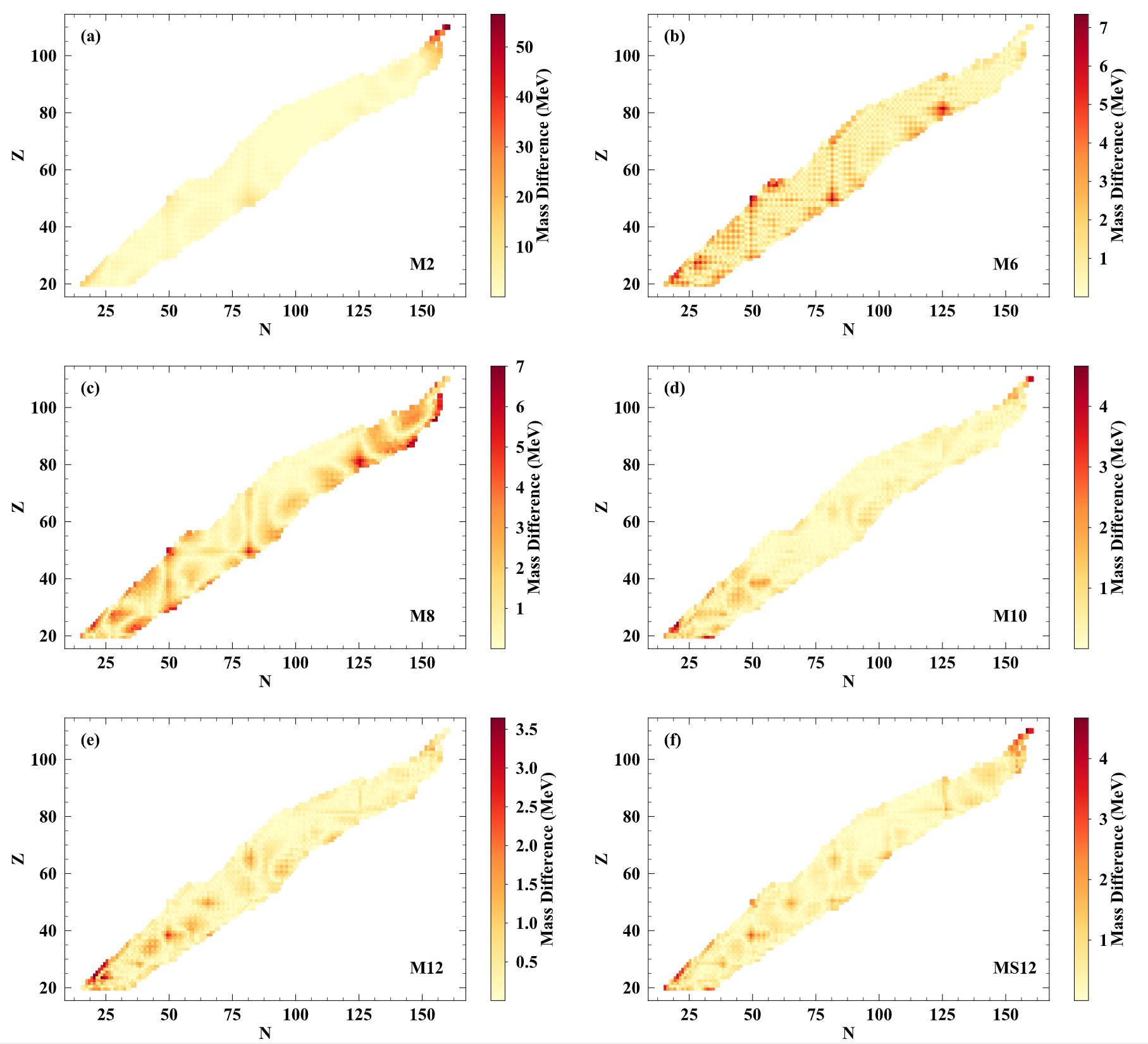
Results across the chart of nuclides with increasing feature space complexity
Note the decrease in the maximum value of the scale
Results: modeling atomic masses
A summary of results
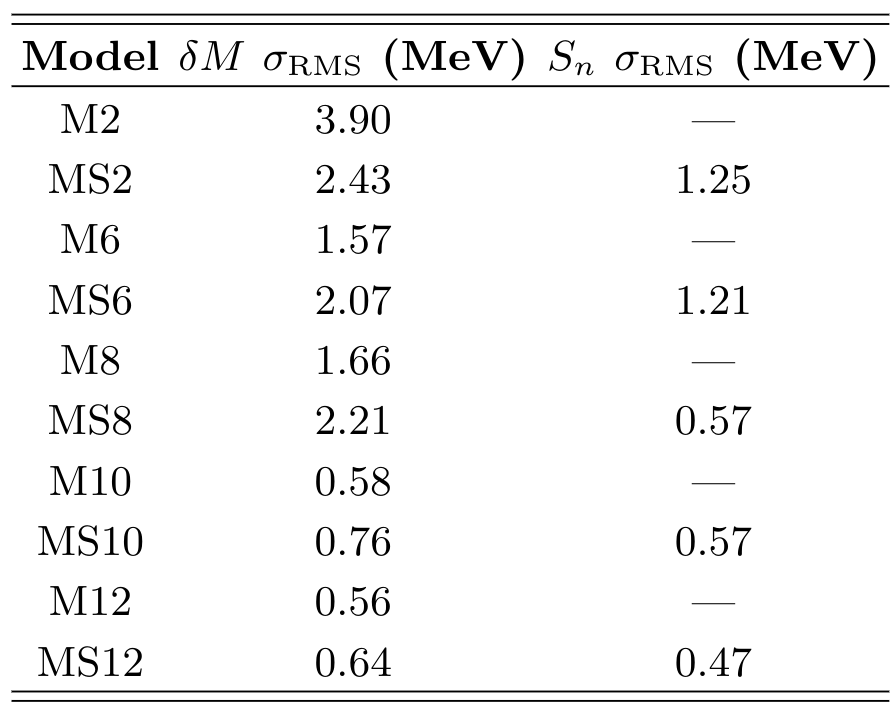
Some lessons learned:
More physics added to the feature space → the better our description of atomic masses
Attempting to fit and predict other mass related quantities (e.g. separation energies) does impact our results
Although marginal compared to choice of feature space
Training on mass data
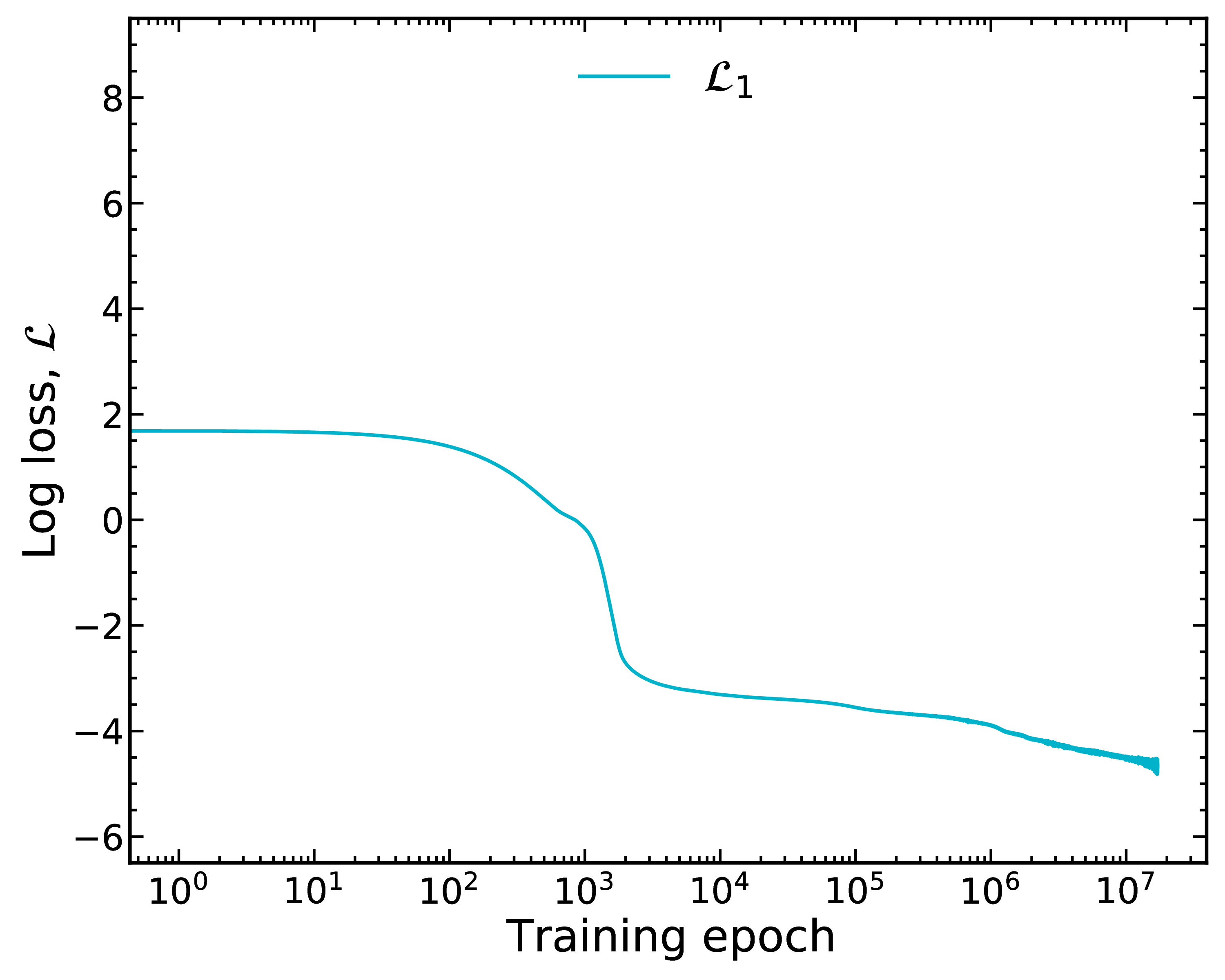
We train on mass data using a log-loss, $\mathcal{L}_1$
Training takes a considerably long time
Introduce physical constraint via loss function
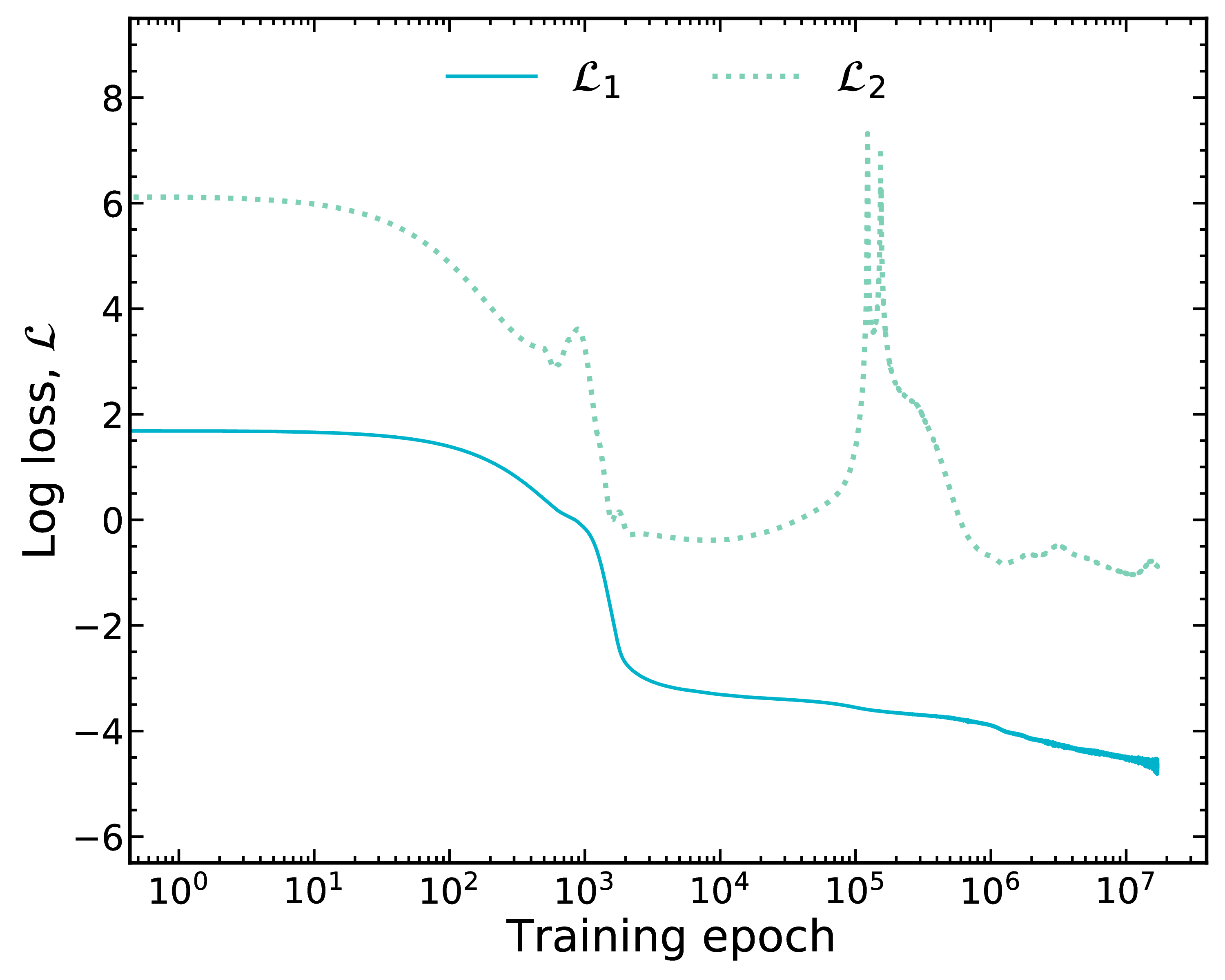
Now we optimize data, $\mathcal{L}_1$, and introduce a second (physical) constraint, $\mathcal{L}_2$
We have tried many physics-based losses, this particular one (Garvey-Kelson relations) performs well
Total loss: sum the two losses
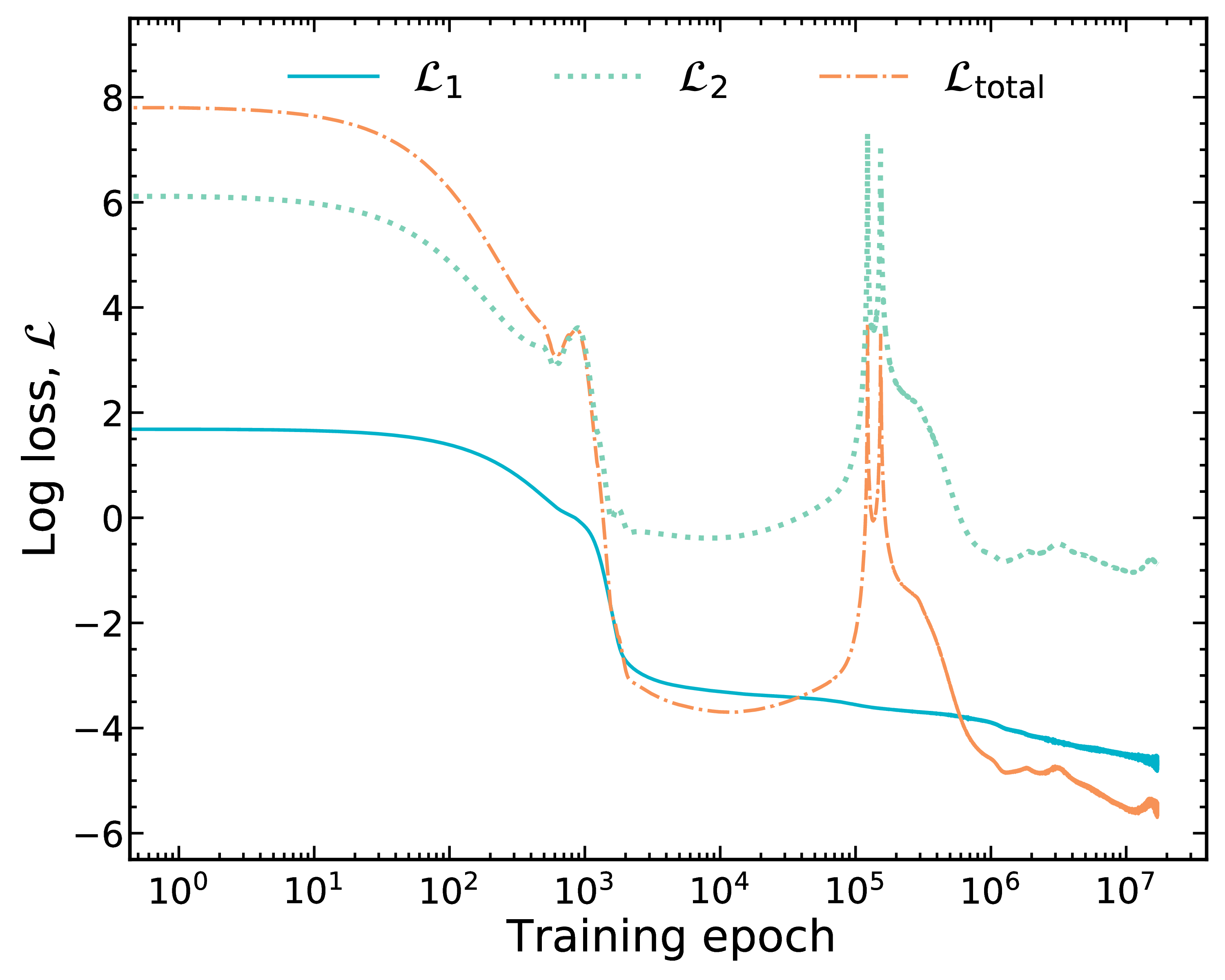
$\mathcal{L}_\textrm{total} = \mathcal{L}_1 + \lambda_\textrm{phys} \mathcal{L}_2$ ; $\lambda_\textrm{phys}=1$ in this case
Good match to data does not imply good physics (although by happenstance it is in the end in this case)!
Mass trends along Nd isotopic chain, $Z=60$
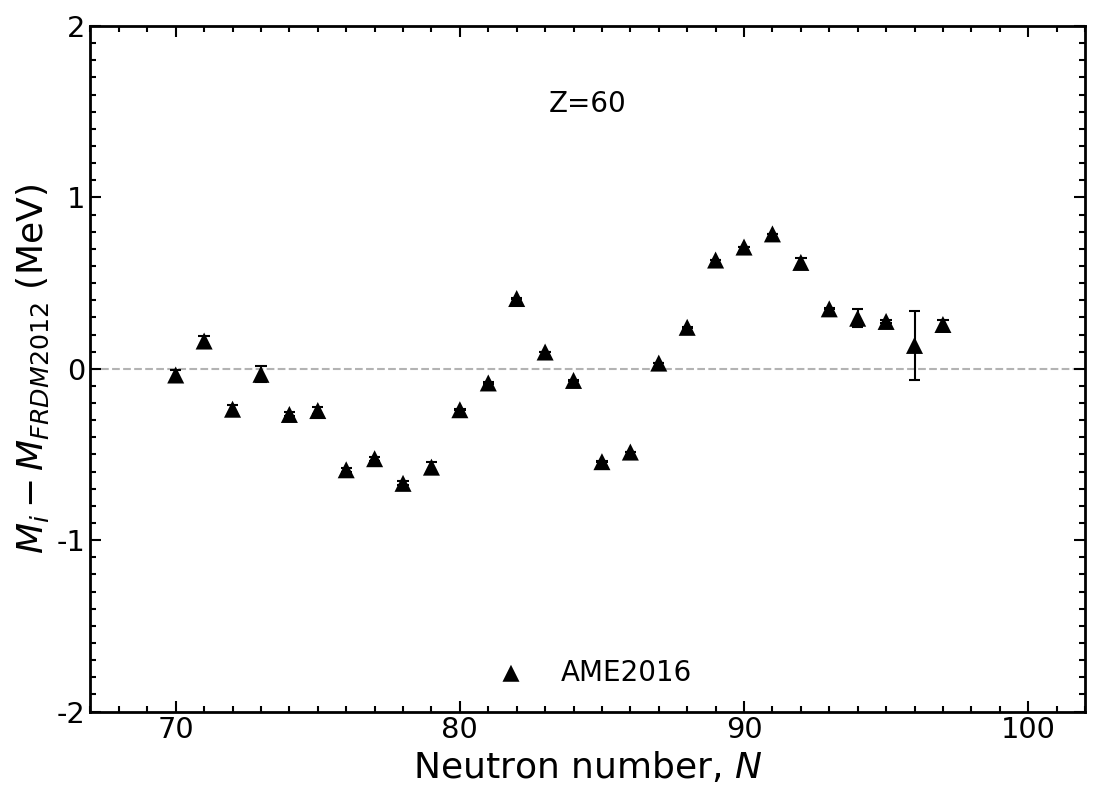
Results plotted relative to the Los Alamos FRDM model
Modern mass models draw a 'straight line' through data
Results of new model Nd, $Z=60$
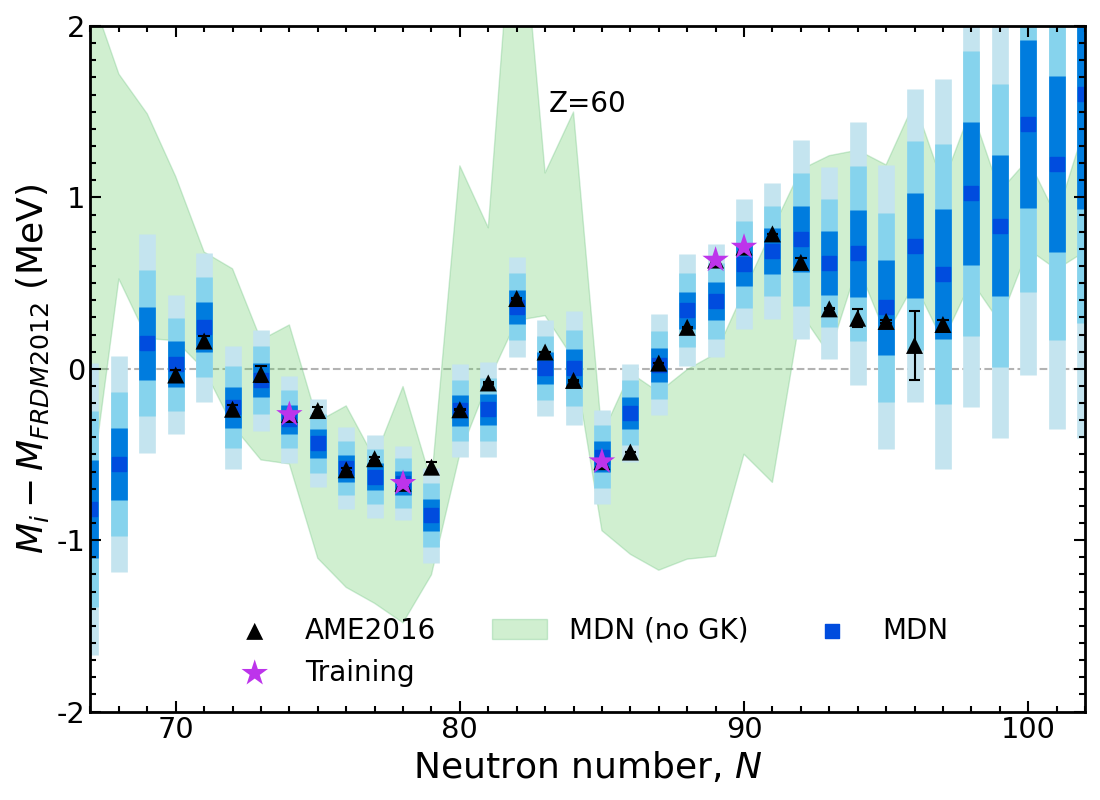
Probabilistic network → well-defined uncertainties predicted for every nucleus ( ◼ 1$\sigma$, ◼ 2$\sigma$ ◼ 3$\sigma$)
Trends in data are captured far better than any mass model
Results of new model Nd, $Z=60$
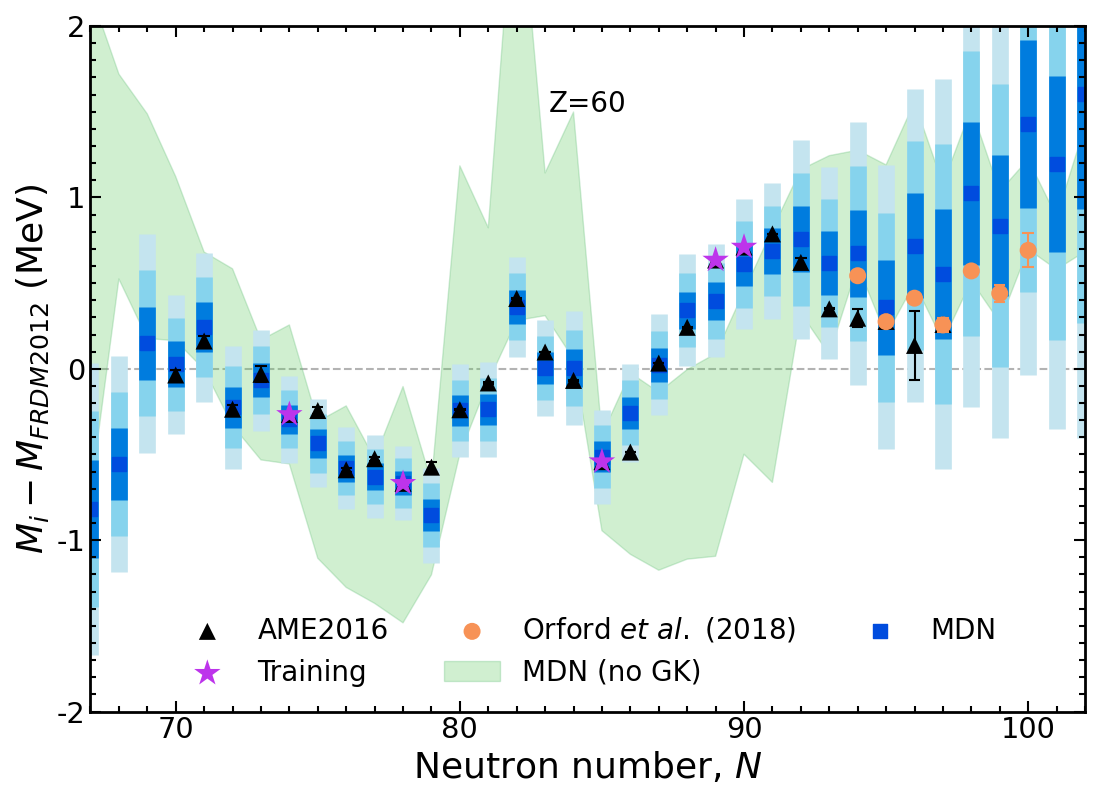
New data (unknown to the model) are in agreement with the MDN model predictions
Model is now trained on only 20% of the AME and predicting 80%!
The training set is random; different datasets perform differently
Results of new model In, $Z=49$
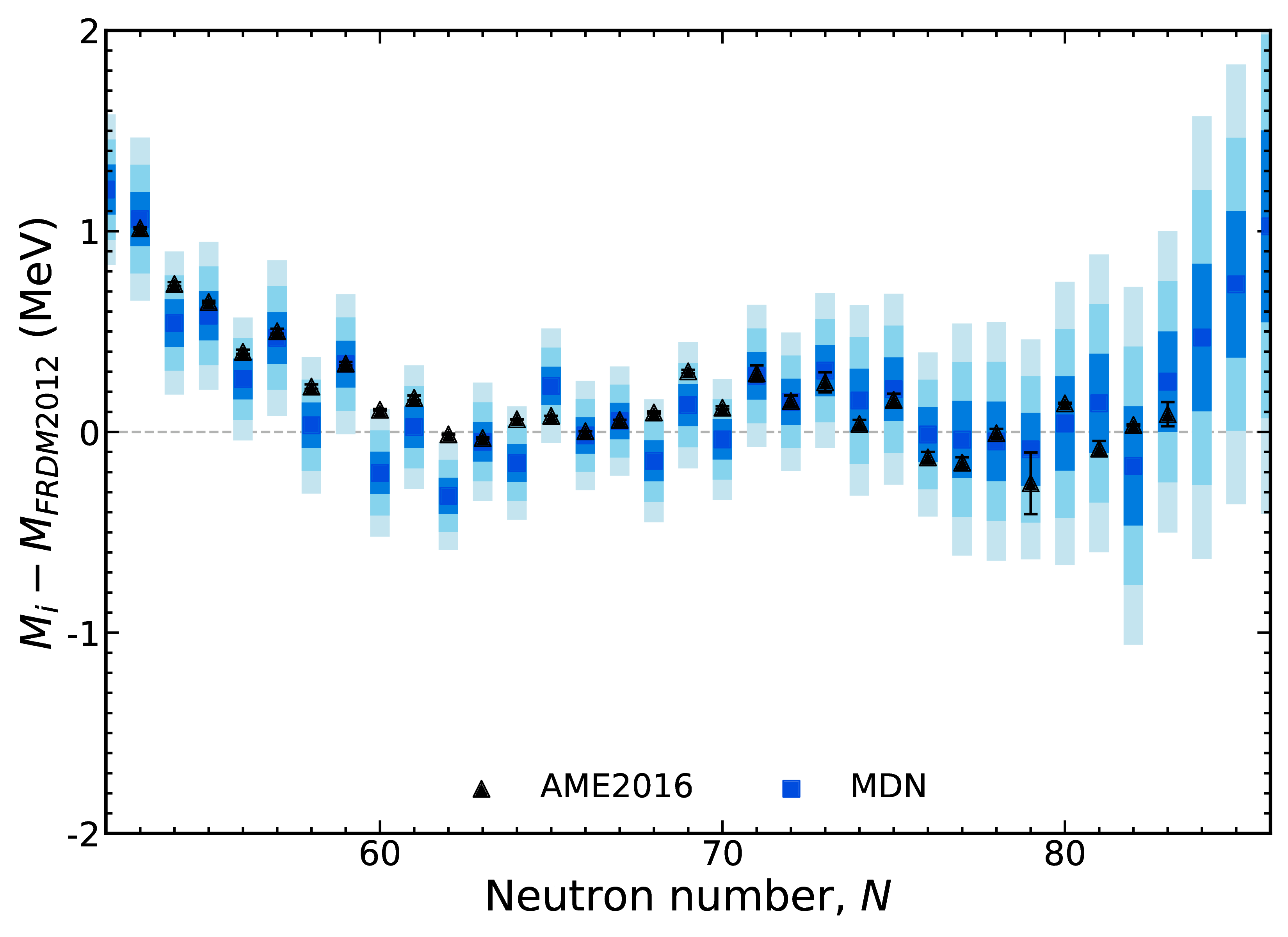
Our results are not limited to any mass region - all of them are described equally well ($Z \geq 20$)
Results are better than any existing mass model; uncertainties inherently increase with extrapolation
We can predict new measurements and capture trends (important for astrophysics)
How can we interpret these results?
One method is to calculate Shapley values (Shapely 1953 • Lundberg & Lee 2017)
Idea arises in Game Theory when a coalition of players (ML - features) optimize gains relative to costs
The players may contribute unequally, but the payoff is mutually beneficial
Applicable to many applications, ML in particular to understand feature importance
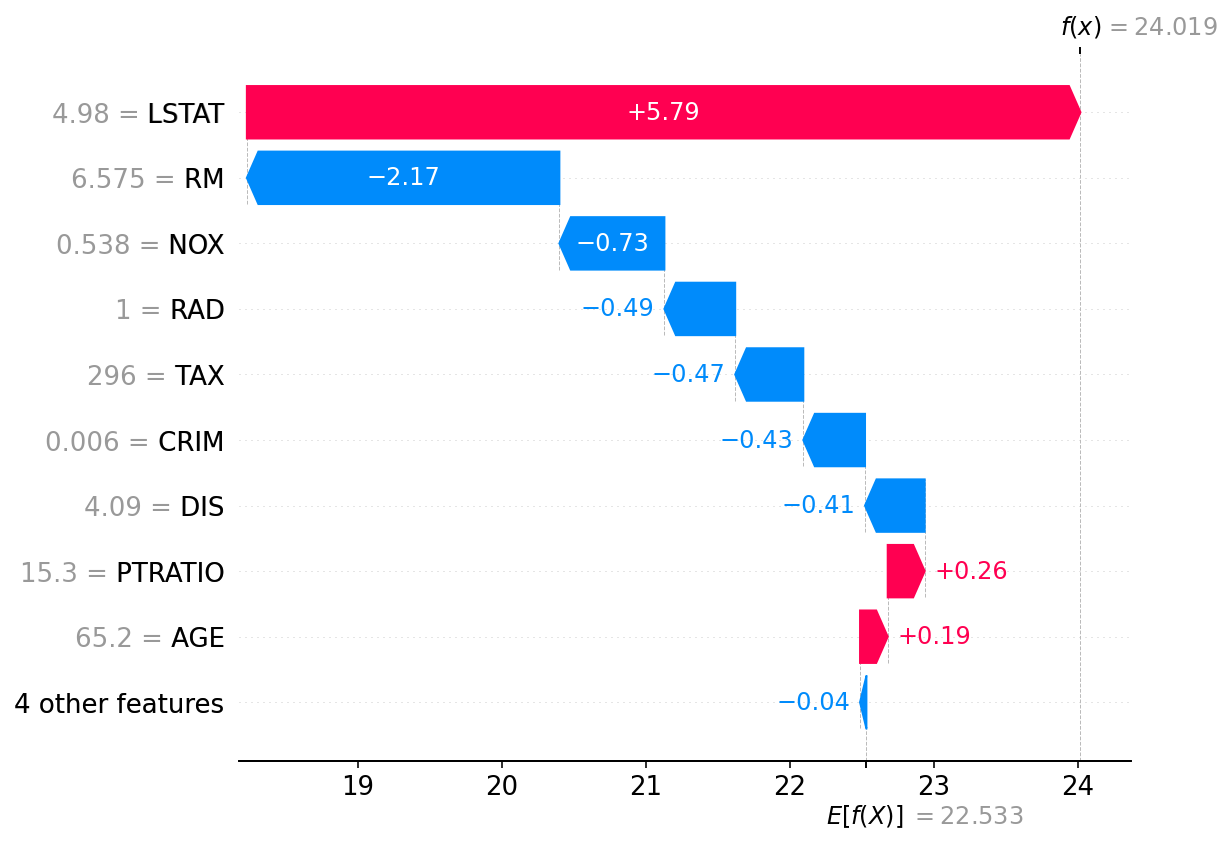
Ranking feature importance
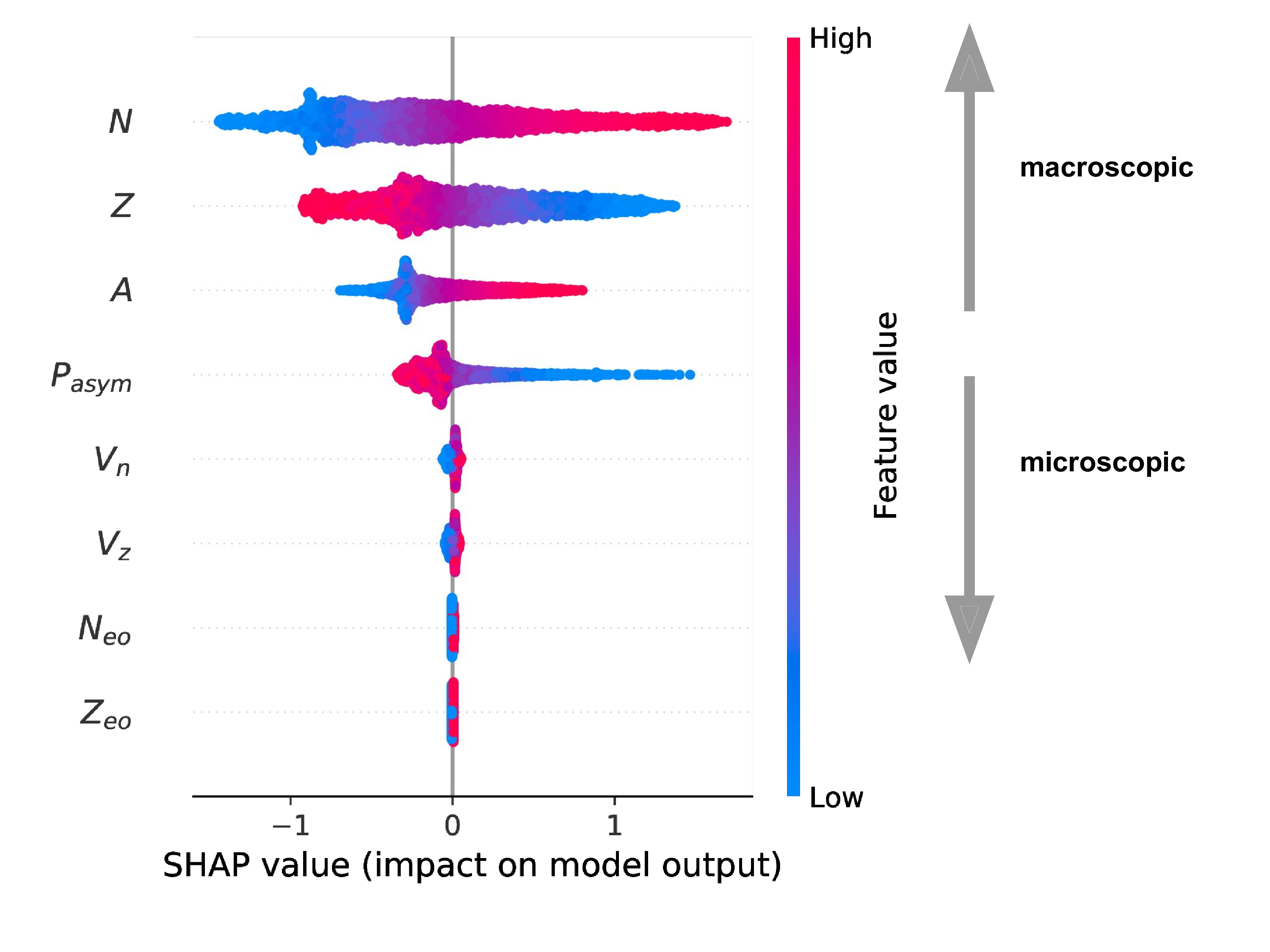
SHAP calculated for all of the AME (2020) [predictions!]
The model behaves like a theoretical mass model
Macroscopic variables most important followed by quantum corrections
What happens when there's new data? (generalization)
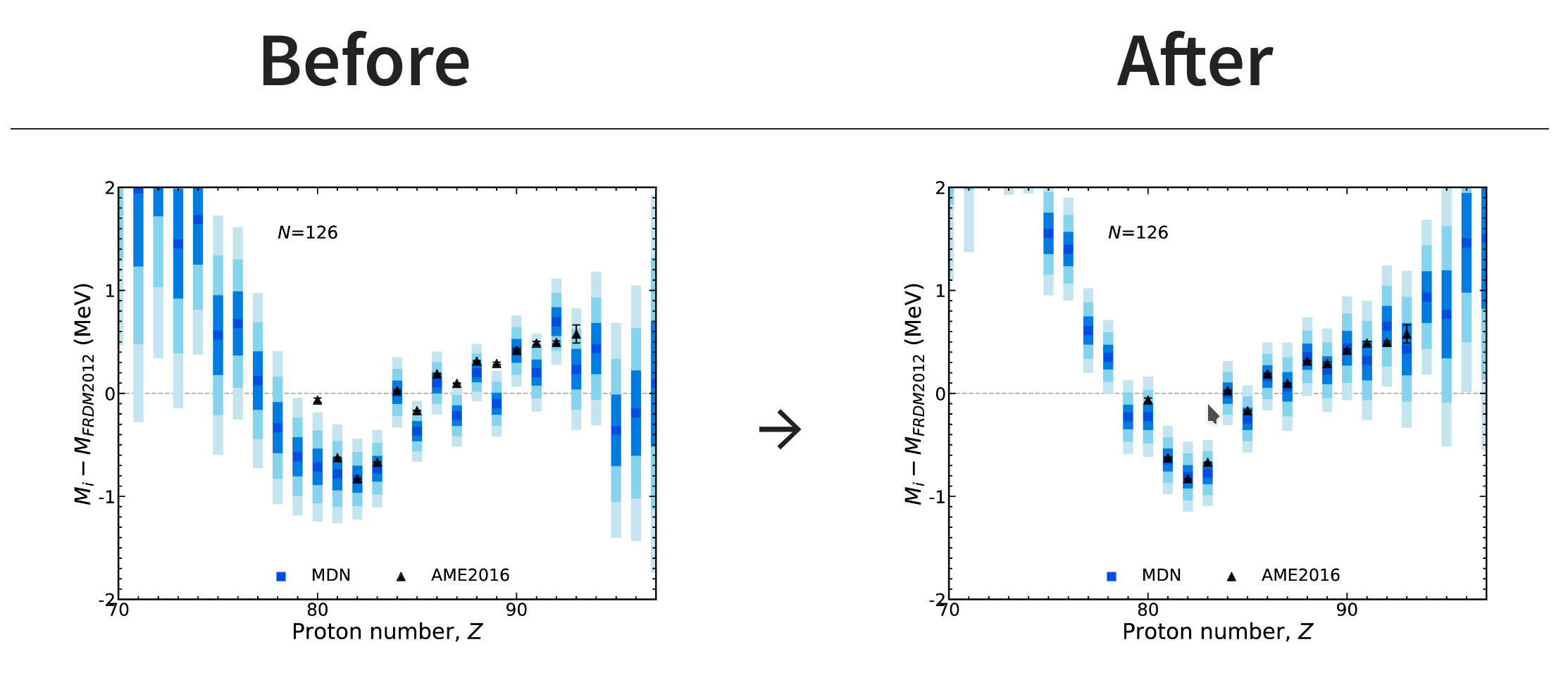
The network is able to incorporate this knowledge and updated predictions via Bayes' theorem
New information provided at closed shell $N=126$
Special thanks to
My collaborators
A. Lovell, A. Mohan, & T. Sprouse
▣ Postdoc

And to my son Zachary for the use of his drawings

Los Alamos National Laboratory Caveat
The submitted materials have been authored by an employee or employees of Triad National Security, LLC (Triad) under contract with the U.S. Department of Energy/National Nuclear Security Administration (DOE/NNSA).
Accordingly, the U.S. Government retains an irrevocable, nonexclusive, royaltyfree license to publish, translate, reproduce, use, or dispose of the published form of the work and to authorize others to do the same for U.S. Government purposes.
Summary
We have developed an interpretable neural network capable of predicting masses
Advances:
We can predict masses accurately and suss out trends in data
Our network is probabilistic, each prediction has an associated uncertainty
Our model can extrapolate and retains the physics
The quality of the training data is important (not shown)
We can classify the information content of existing and future measurements with this type of modeling
We are now ready to study the impact of this modeling in astrophysics!
Results / Data / Papers @ MatthewMumpower.com
