Mumpower HTML Presentation

Fission across the chart of nuclides
and implications for the $r$ -process

LA-UR-19-30940

Matthew Mumpower

Workshop on nuclear fission dynamics

Monday Oct. 28 $^{th}$ 2019

FIRE Collaboration
Fission In R-process Elements

To understand the formation of the elements

Requires deep knowledge of a range of fields, including:

The theoretical modeling of astrophysical environments

Multi-messenger observations (gravitational waves, EM waves, etc.)

Nuclear theory predictions for exotic nuclei

Precision experiments to constrain nuclear theory

Data and observations are limited

We must be clever when deciphering what is going on with nucleosynthesis...

What is the $r$ -process?

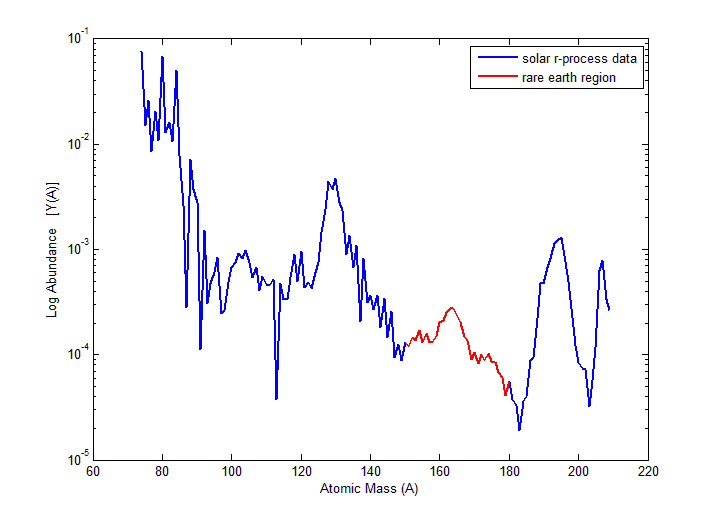
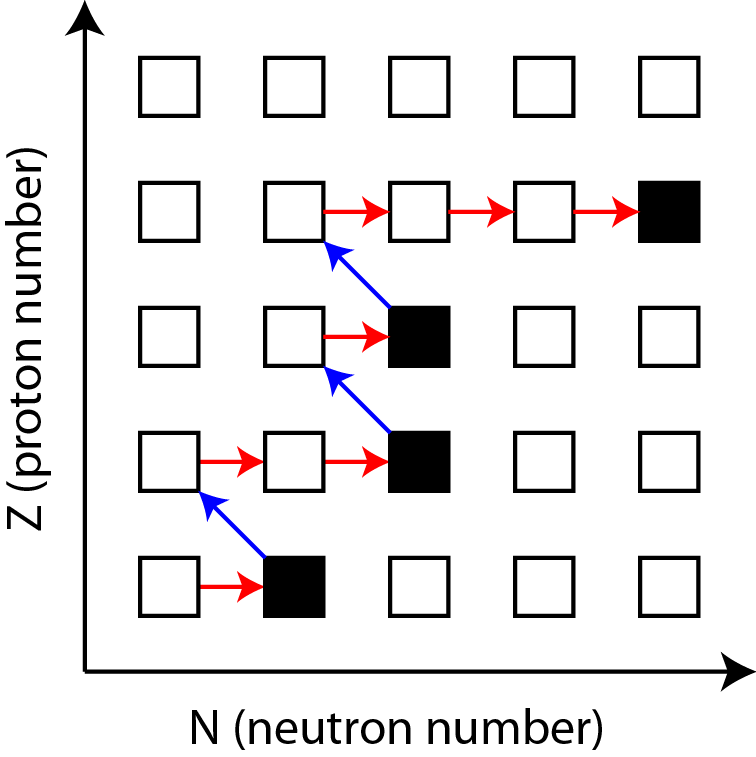
Rapid neutron capture that occurs in astrophysical environments allowing for the production of heavy elements

Neutron captures are initially much faster than $\beta$ -decays

Relative slowdown in the nuclear flow (right) produces peak structures in the observed abundances (left)

Astrophysical environment must produce a lot of free neutrons in order for this process to proceed

Aprahamian et al. (2018) • Horowitz et al. J Phys G 083001 (2019)

Where can the $r$ -process occur?

One possibility is in (rare?) supernovae

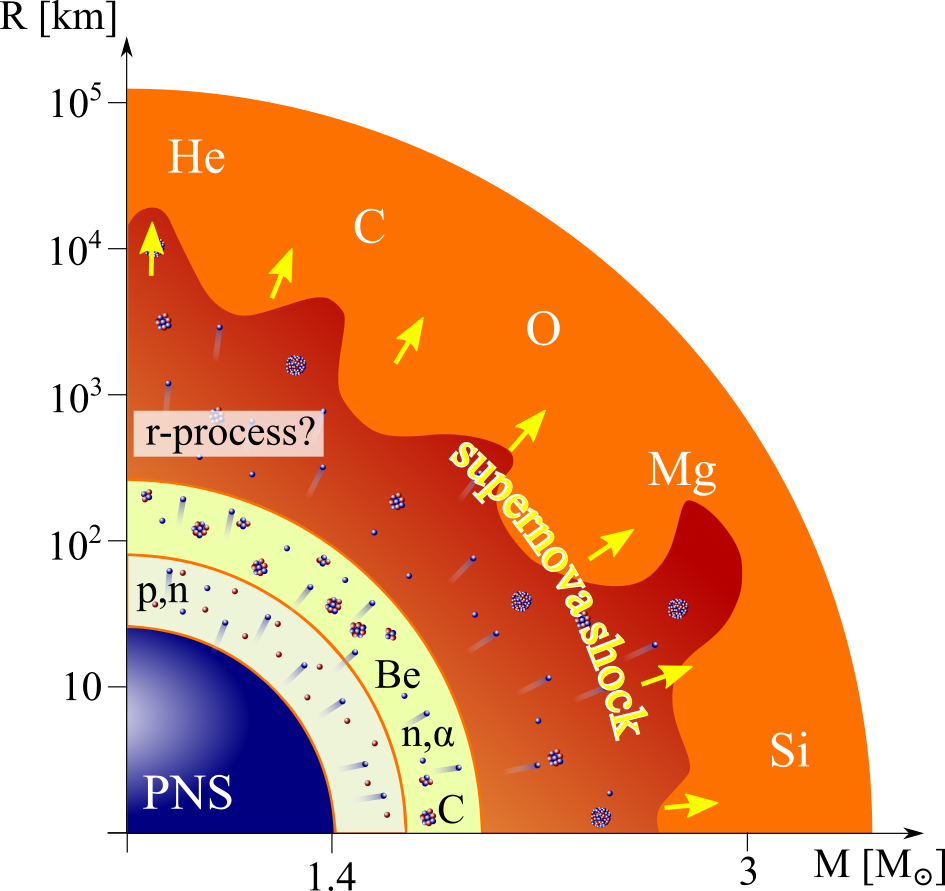
For standard supernovae (left) neutrino physics still needs to be well understood

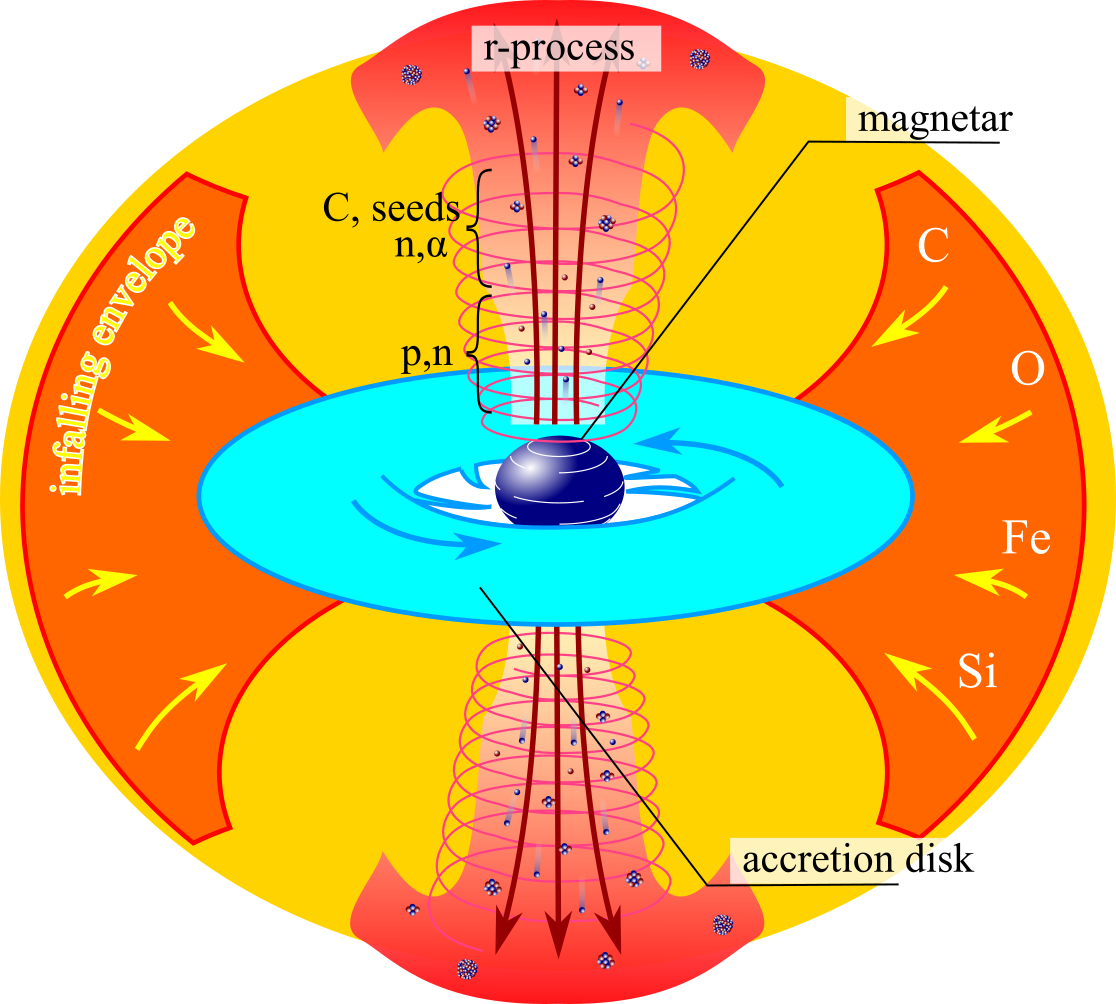
Jets in magnetorotational driven supernovae (right) may also provide the necessary conditions

Another option is the disk winds of collapsars - black hole forms after core collapse of a rapidly rotating star

Meyer ApJ (1989) • MacFadyen & Woosley ApJ (1999) • Figure from Mumpower et al. in prep. (2019)

Where can the $r$ -process occur?

Another possibility is in compact object mergers

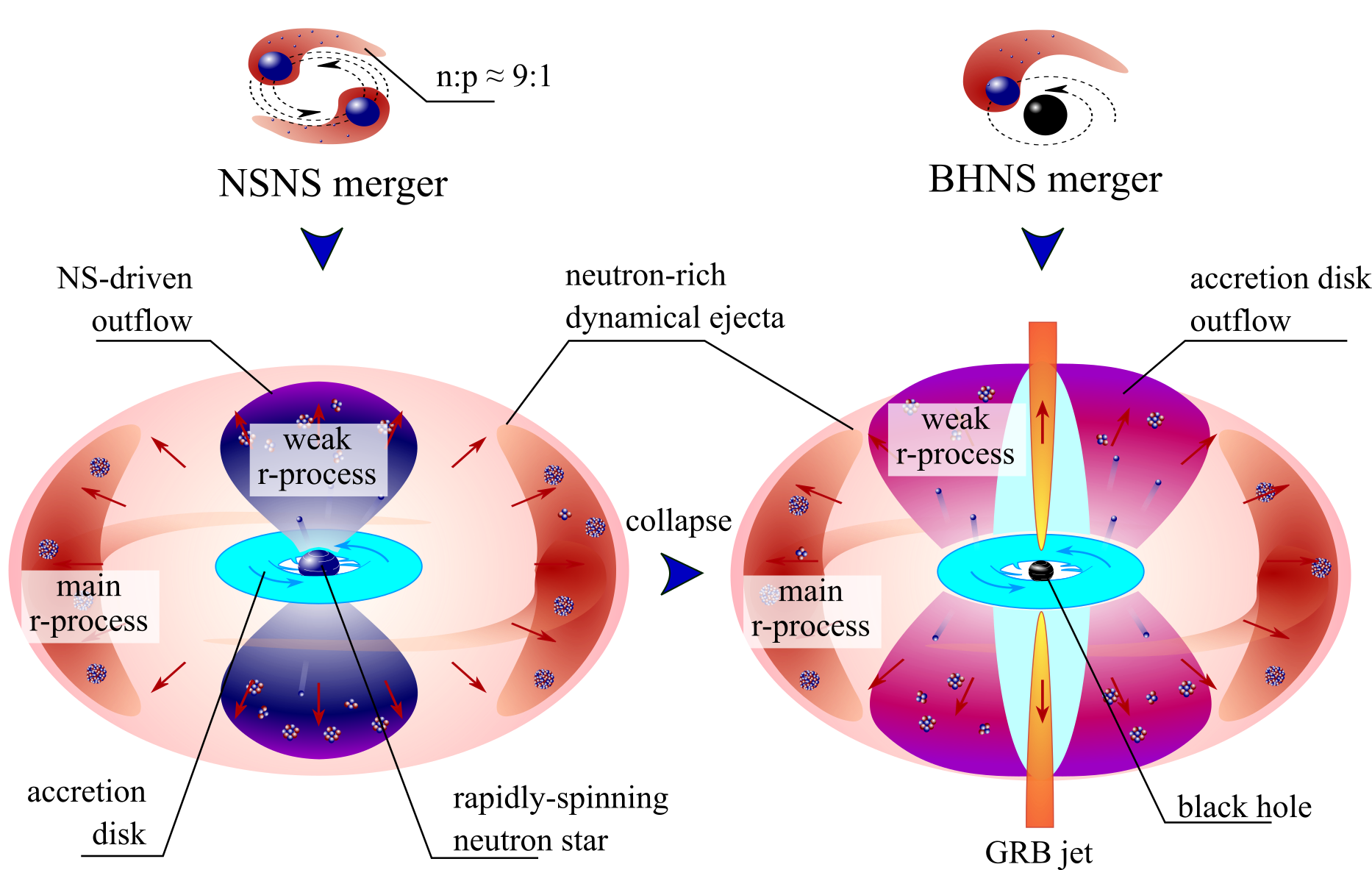
A binary merger of neutron stars is an exciting possibility (some indirect evidence exists)

Another option is in the disk of a black hole neutron star binary

Lattimer & Schramm (1974) • Korobkin et al. (2012) • Figure from Mumpower et al. in prep. (2019)

When we model nucleosynthesis

We want to describe the abundances observed in nature

But there is uncertainty in:

The astrophysical conditions (large variations in current simulations)

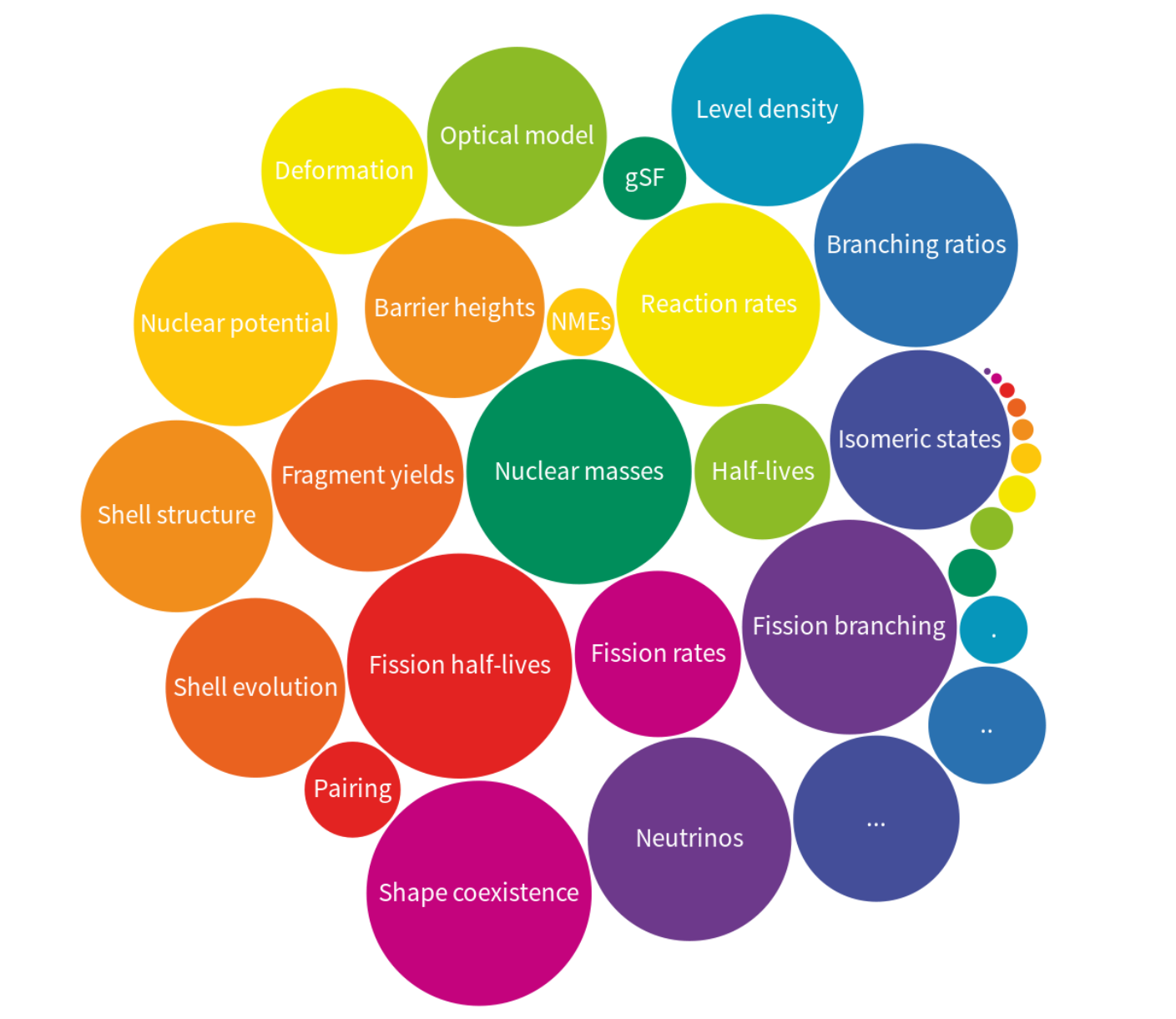
The nuclear physics inputs (1000's of unknown species / properties)

Mumpower et al. PRC (2015) • Côté et al. ApJ (2018)

Inputs from nuclear physics

1st order: masses, $\beta$ -decay rates, reaction rates & branching ratios

Dillmann et al. EPJA (2002) • Aprahamian et al. (2018) • See review paper: Mumpower et al. PPNP 86 (2016)

$r$ -Process Calculation

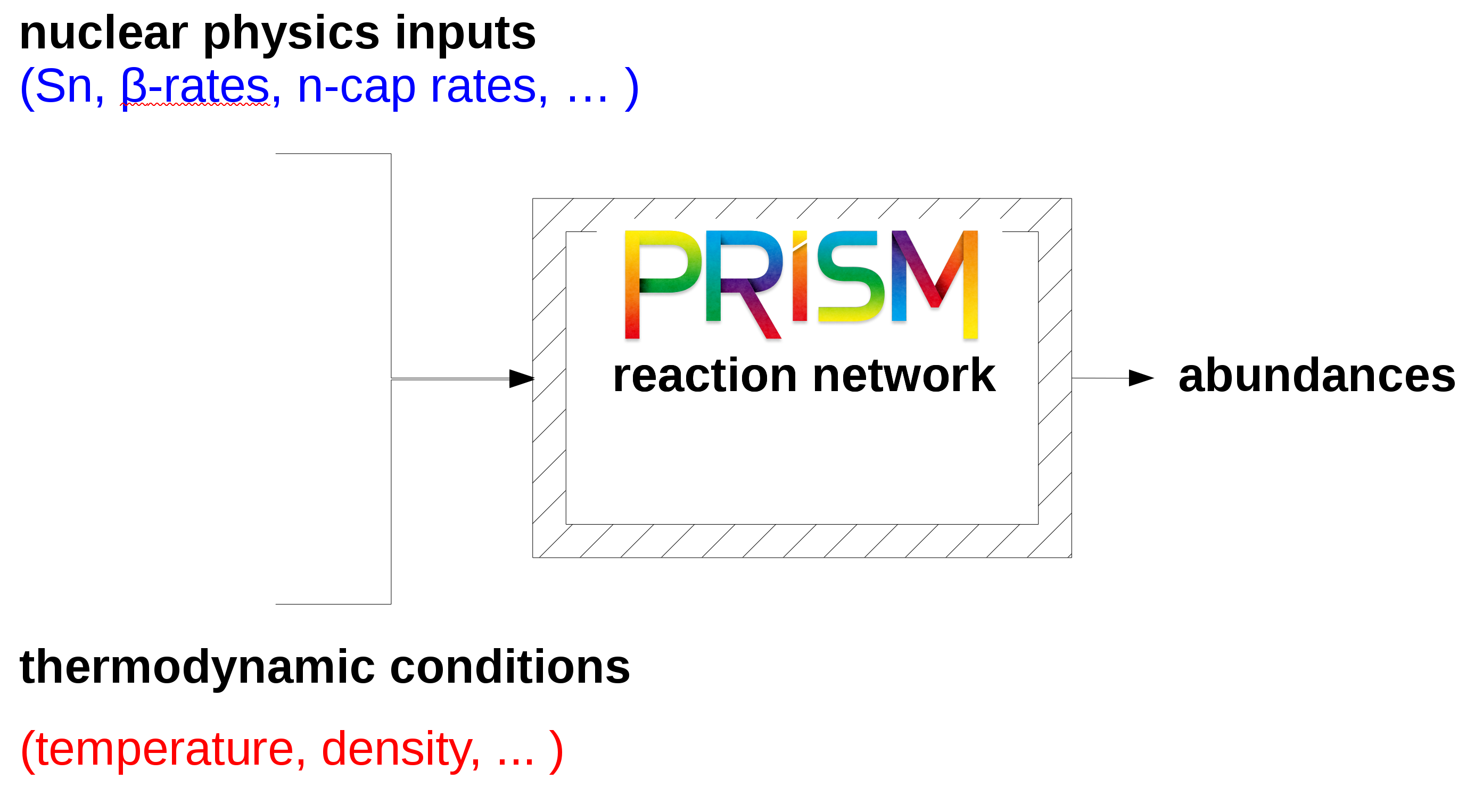
PRISM: Portable Routines for Integrated nucleoSynthesis Modeling

Sprouse & Mumpower in prep (2019)

Nuclear fission in a nutshell

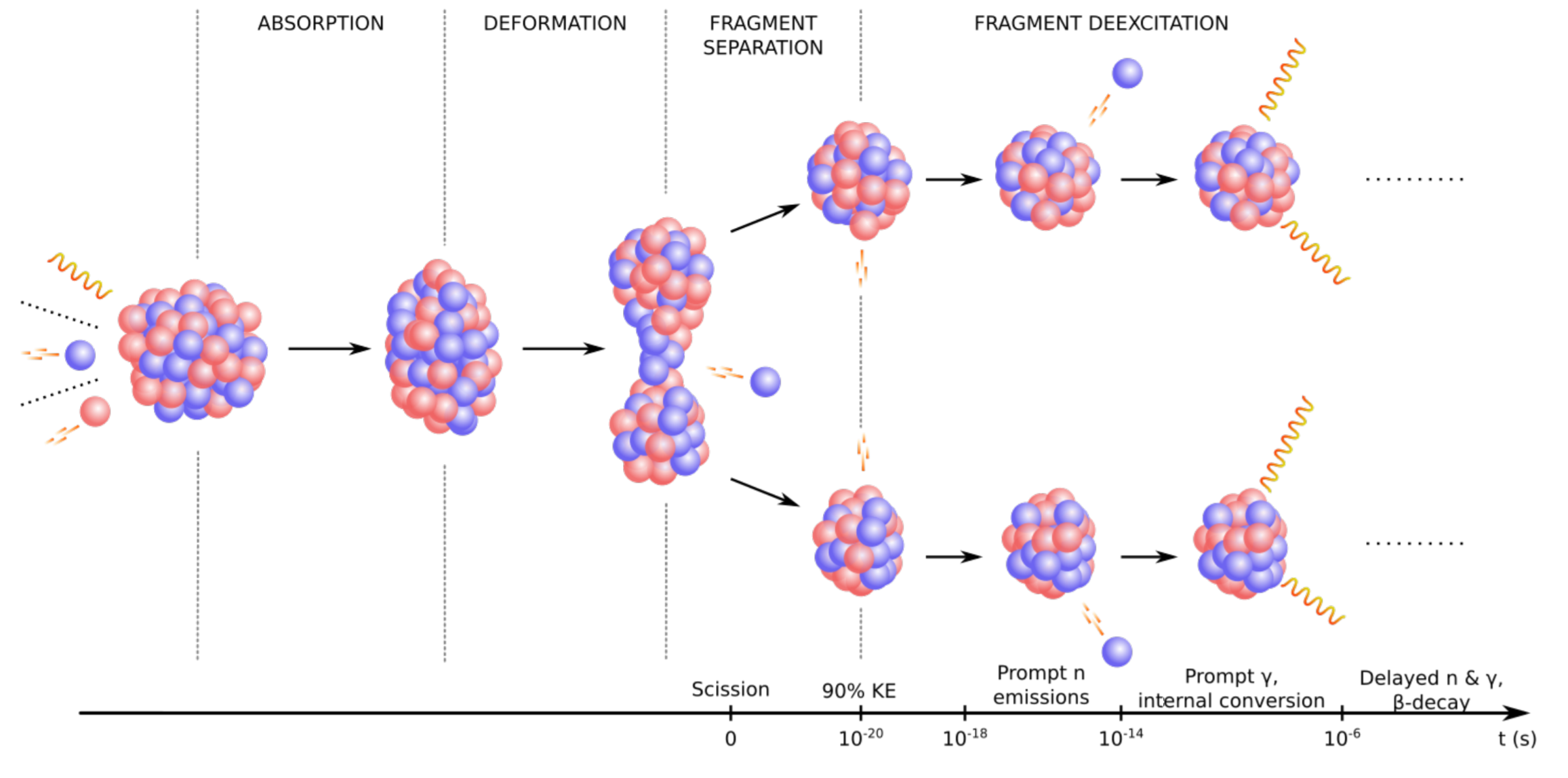
The fission process:

A heavy nucleus splits into two lighter fragments

Subsequent particle emission and decays then occur

Many events gives rise to fission yield

Meitner & Frisch (1938) • Bohr & Wheeler (1939) • Figure from Verriere et al. in prep. (2019)

Nuclear fission for the $r$ -process

Influence on the $r$ -process:

Fission rates and branching determine re-cycling (robustness)

Fragment yields place material at lower mass number; barriers determine hot spots

Large Q-value ⇒ impacts thermalization and therefore possibly observations

Responsible for what is left in the heavy mass region when nucleosynthesis is complete ⇒ "smoking gun"

Holmbeck et al. ApJ 870 1 (2019) • Vassh et al. J. Phys. G (2019) • Figure from Verriere et al. in prep. (2019)

Fission Barriers

Fission Barrier Heights (FRLDM)

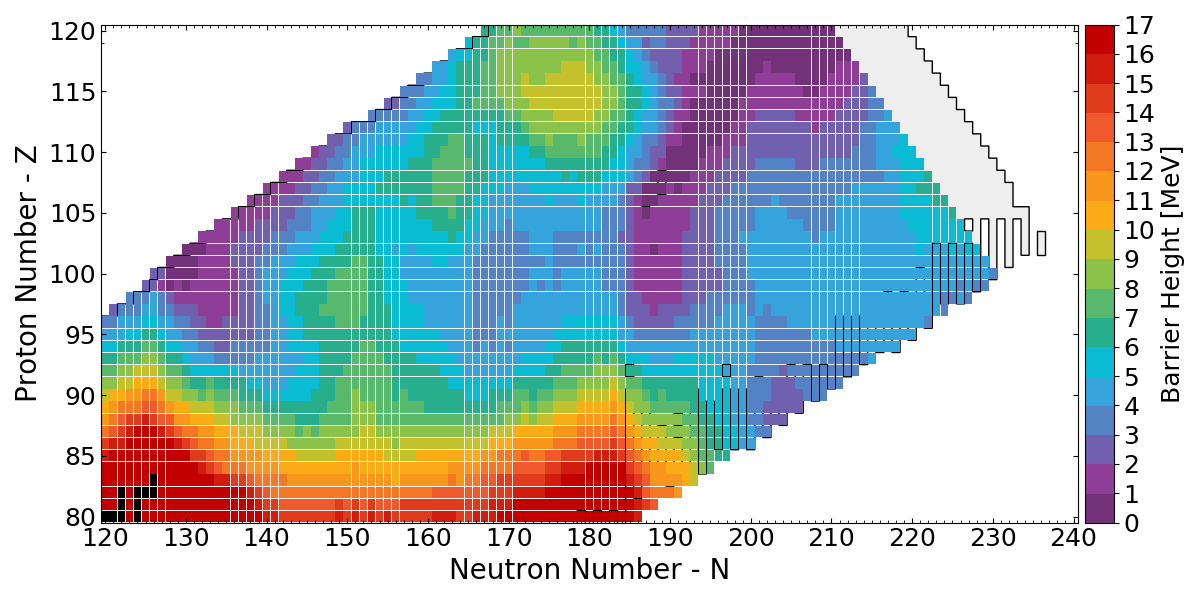
(Maximum) FRLDM Barrier heights

Low barrier ↦ fission ⇑

$r$ -process hot spots follow low barriers

Möller et al. PRC 91 024310 (2015)

Fission Barrier Heights (HFB-14)

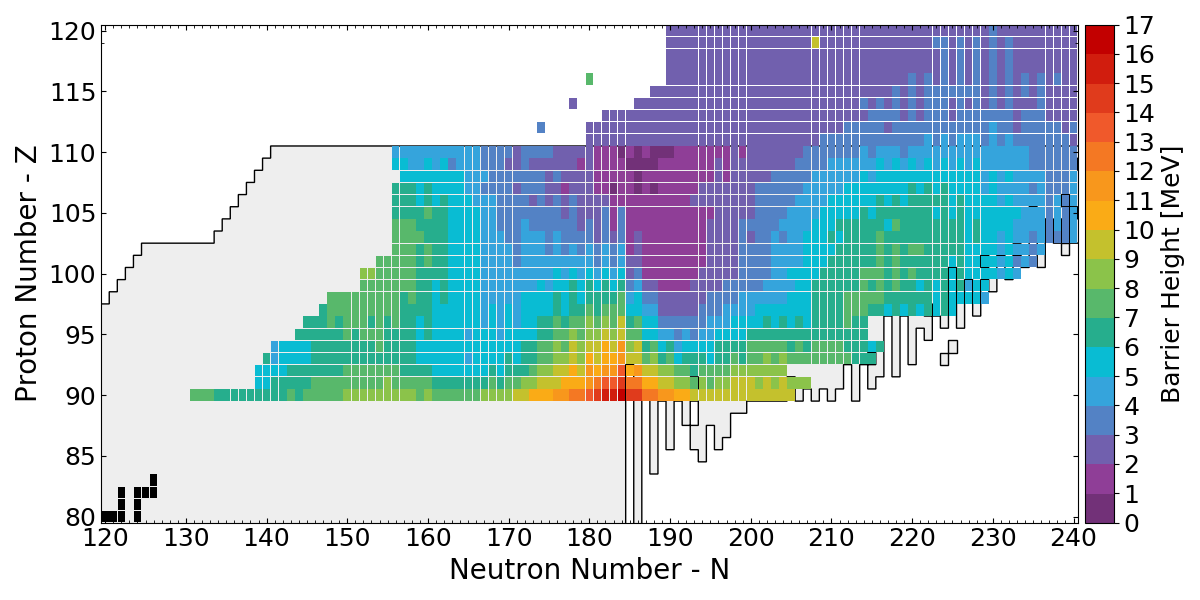
(Maximum) HFB-14 Barrier heights

Low barrier ↦ fission ⇑

Used in (n,f) and $\beta$ df calculations

http://www.astro.ulb.ac.be/pmwiki/Brusslib/HomePage

Fission hot spots

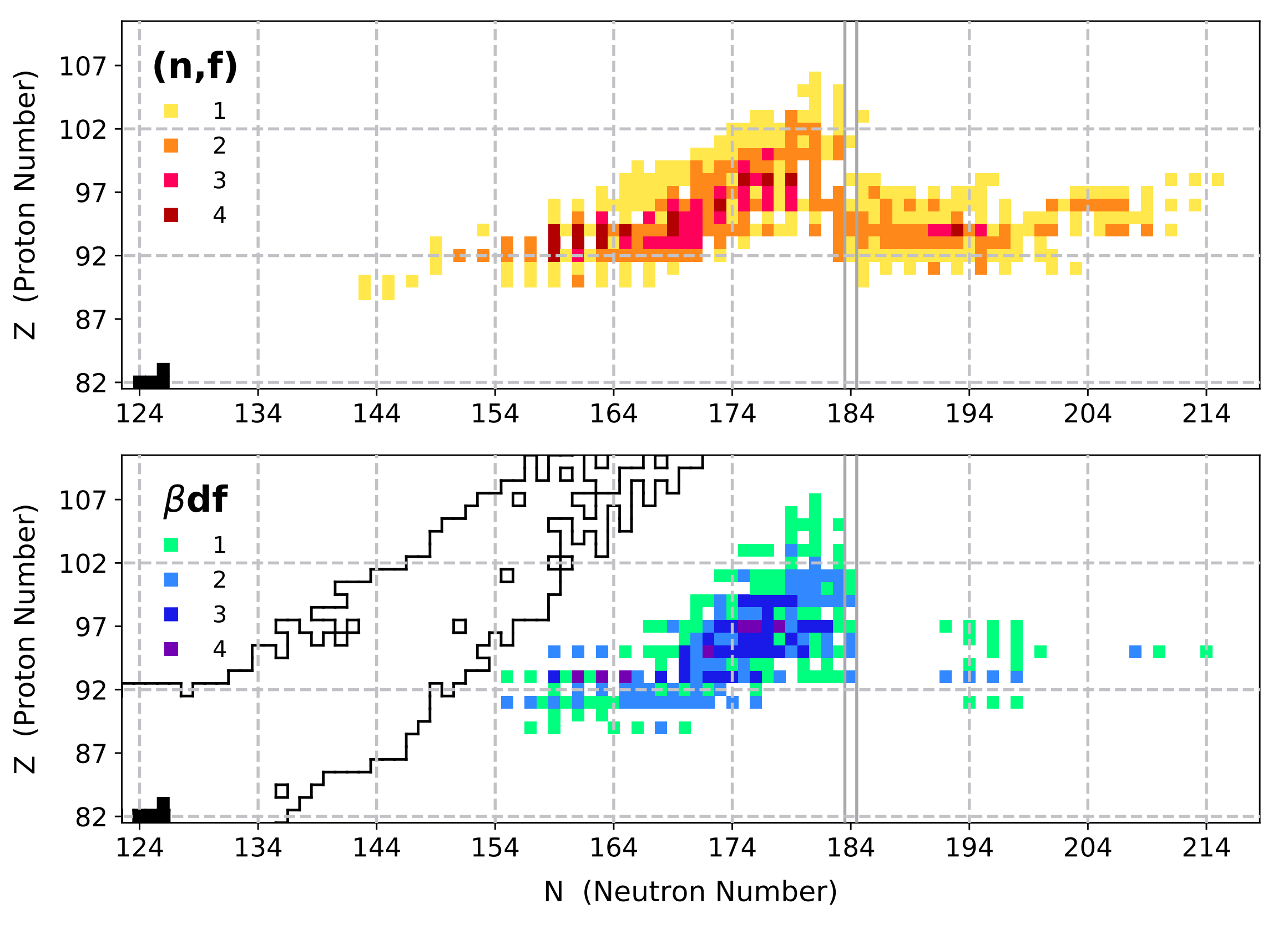
We've taken a look at the region where fission seems to occur the most

With variations in both astrophysical conditions and nuclear models

Nuclei which influence the final abundances are colored for (n,f) and ( $\beta$ ,f)

Vassh et al. J. Phys. G (2019)

Neutron-induced Fission

Neutron-induced fission theory

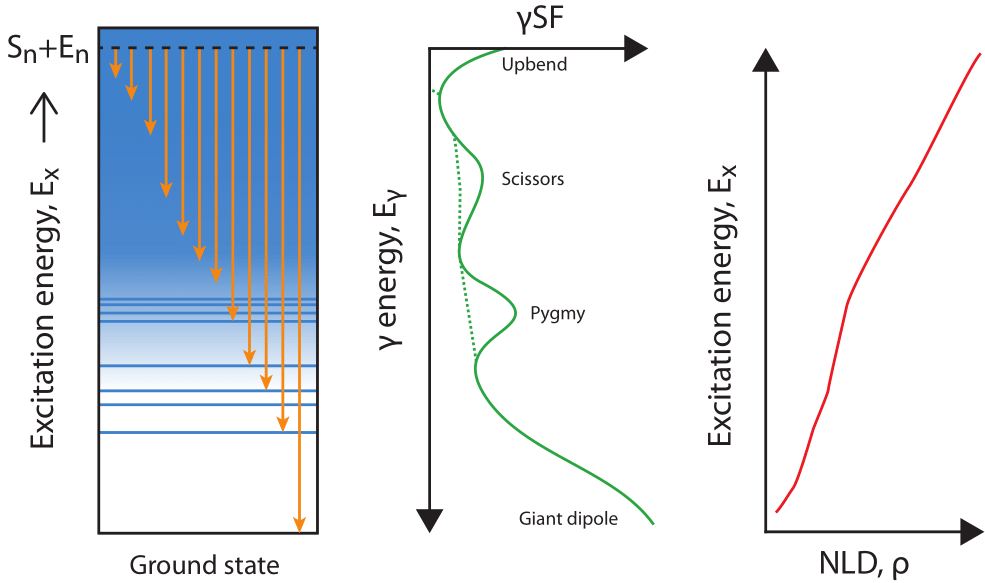
We use statistical Hauser-Feshbach theory updated to account for fission transmission

Model inputs: nuclear level density, $\gamma$ -ray strength functions, optical model potentials and fission barriers

Kawano et al. PRC 94 014612 (2016) • Mumpower & Kawano in prep. (2019)

Neutron-induced fission

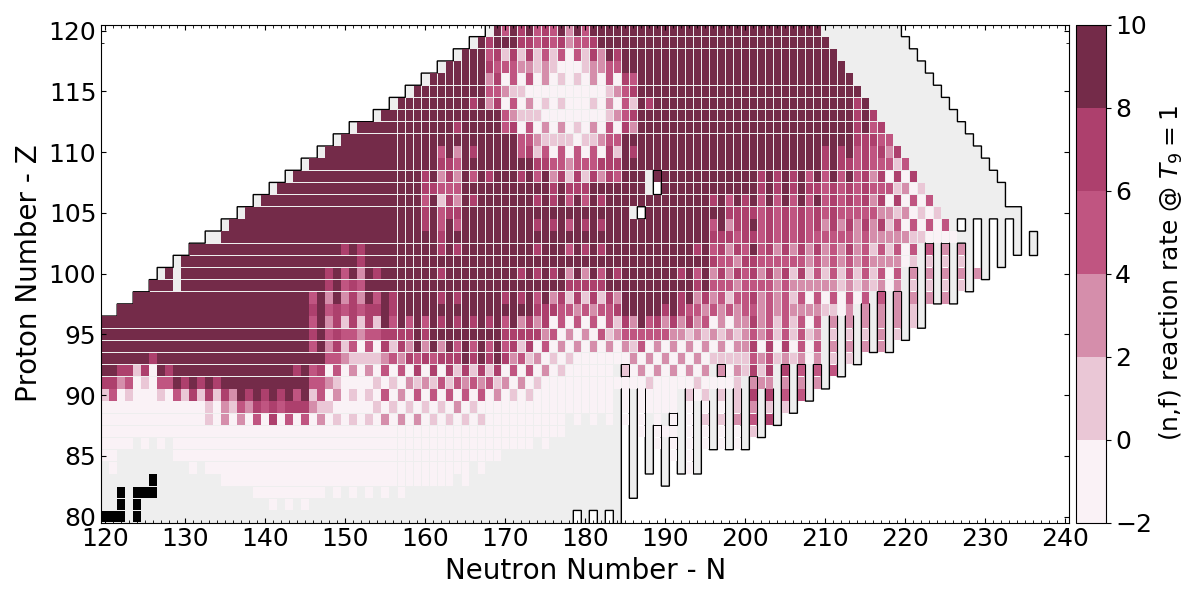
Use statistical Hauser-Feshbach for competition between neutrons, $\gamma$ s and fission

Barrier heights Möller (2015) / FRDM2012 masses

Large region that will fission cycle $r$ -process

Mumpower & Kawano in prep. (2019)

Neutron-induced fission

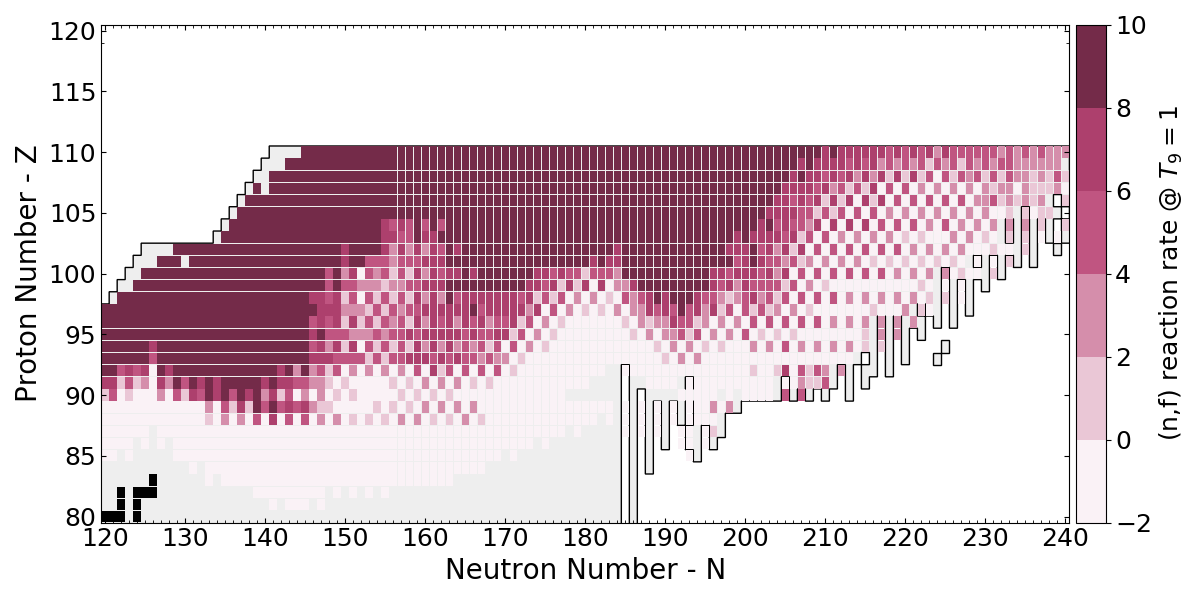
Use statistical Hauser-Feshbach for competition between neutrons, $\gamma$ s and fission

Barrier heights from HFB-14 / HFB-17 masses

Similar results are obtained for other nuclear models

Mumpower & Kawano in prep. (2019)

$\beta$ -decay & $\beta$ -delayed fission

Combining QRPA + HF

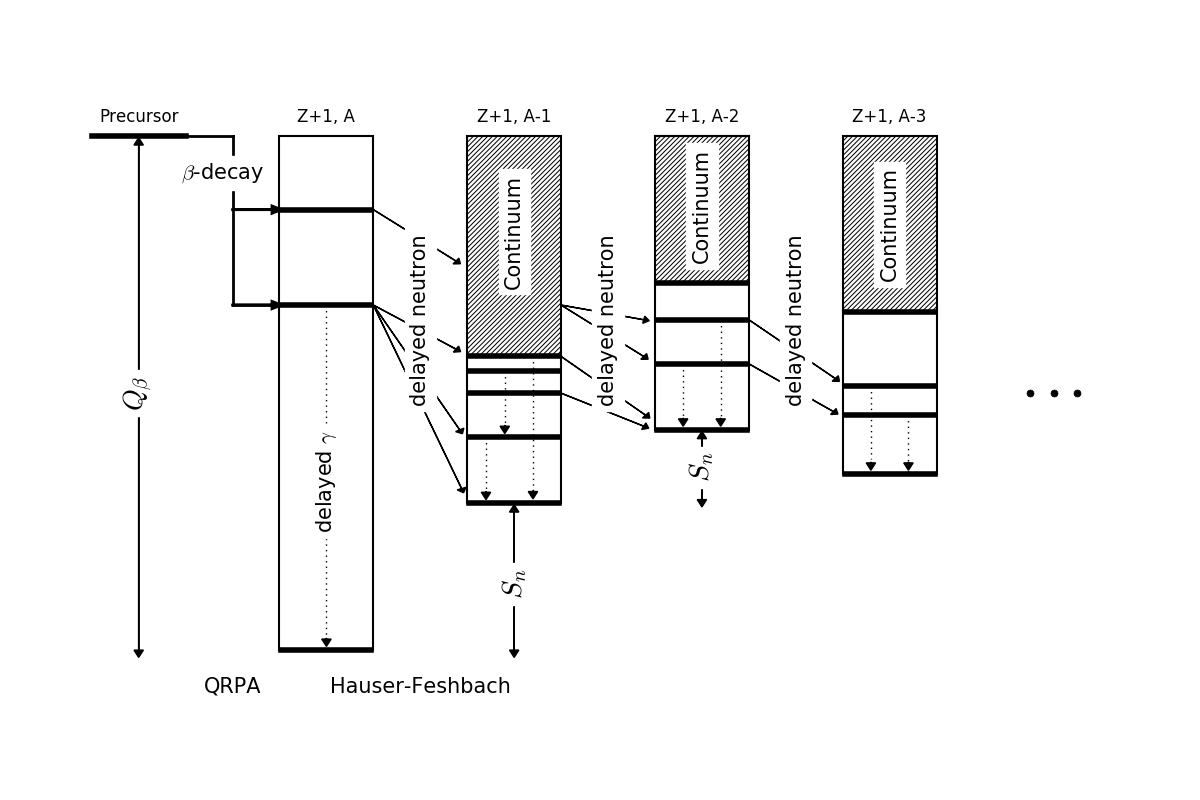
Initial population from the $\beta$ -decay strength function from P. Möller's QRPA

Follow the statistical decay until all excitation energy is exhausted

Möller et al. PRC (1997 & 2003) • Kawano et al. PRC 94 014612 (2016) • Mumpower et al. PRC 94 064317 (2016)

Average neutron emission

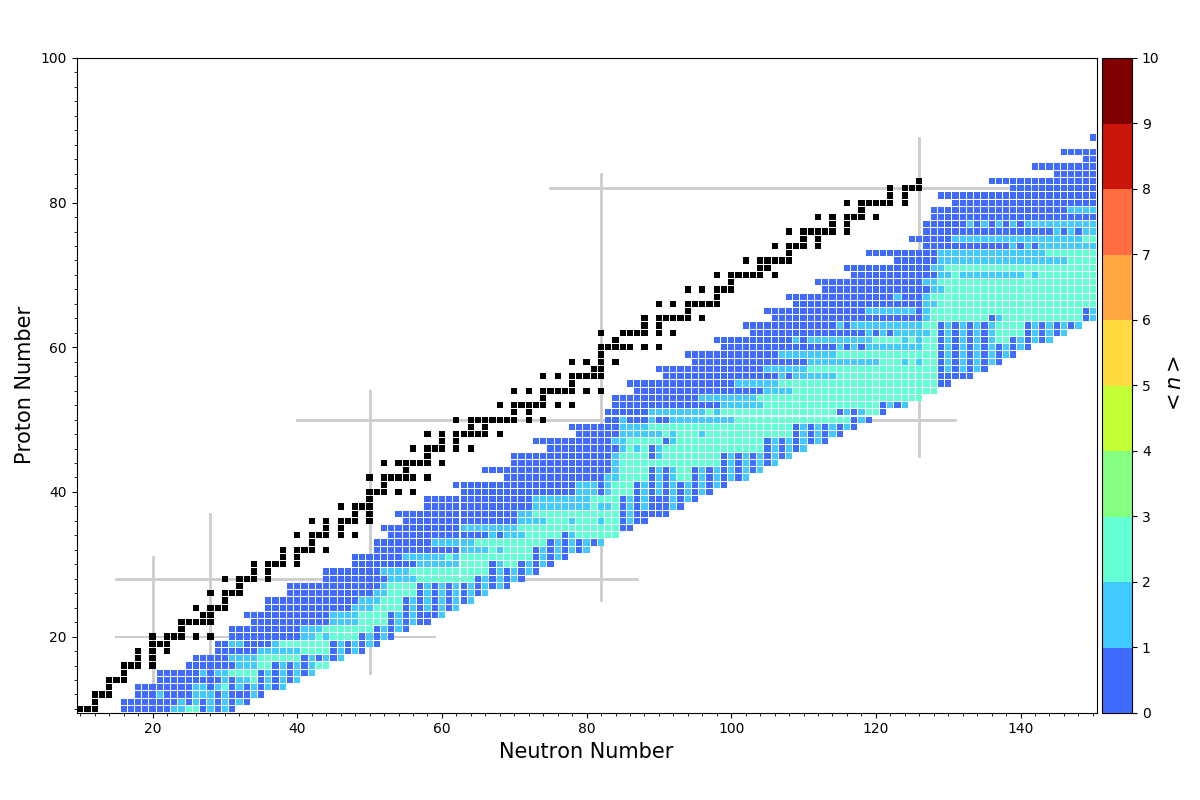
Apply energy window method to the entire chart of nuclides

Problem with describing very neutron-rich nuclei

Mumpower et al. PRC 94 064317 (2016)

Average neutron emission

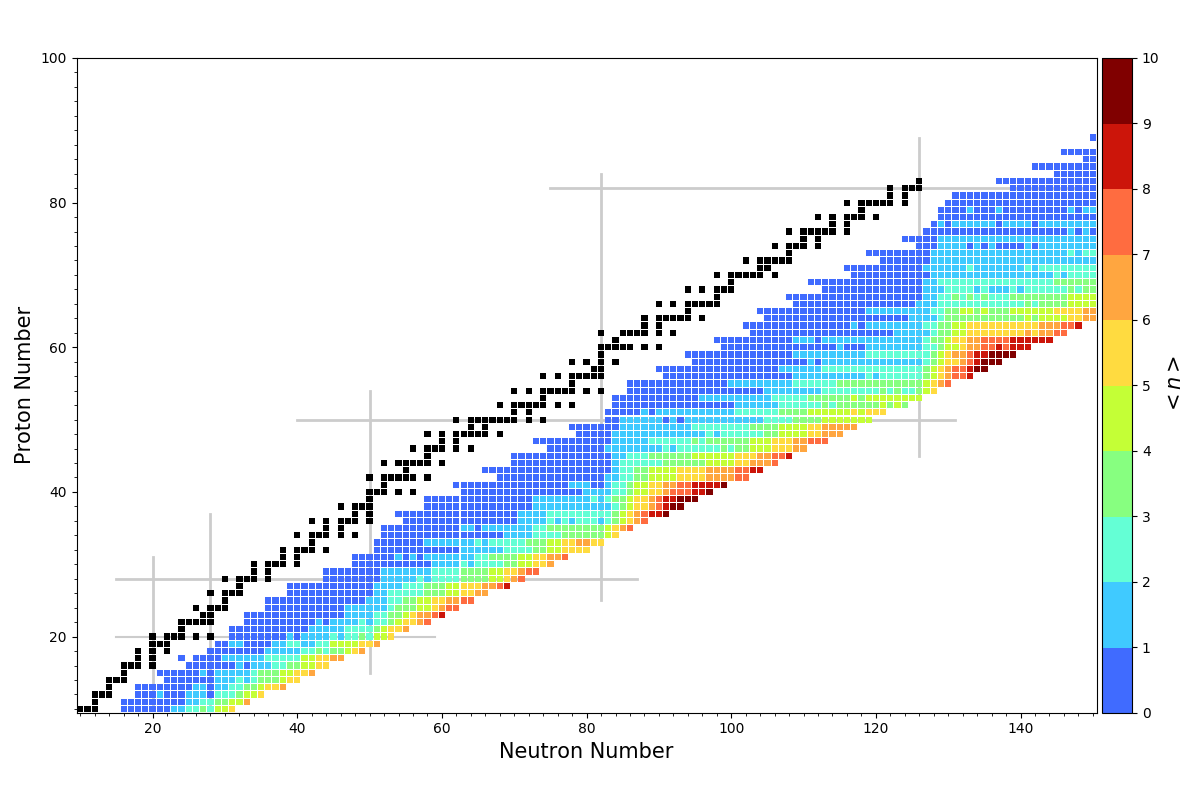
Apply the QRPA+HF method to the entire chart of nuclides

Problem with neutron-rich nuclei goes away

Mumpower et al. PRC 94 064317 (2016) • Möller et al. ADNDT (2018)

Extensive benchmarking

QRPA+HF GT-only $\beta$ -strength are within of measured $P_{1n}$ values

Adding FF transitions improves the match to measured data by 3%

Using measured masses improves the match to measured data by 3%

This yields a roughly global model uncertainty to measured $P_{1n}$ values
The best in the business!

Can we extend this model to other phenomena ... fission?

Spyrou et al. PRL 117 142701 (2016) • Mumpower et al. PRC 94 064317 (2016) • Wu et al. PRL 118, 072701 (2017)

$\beta$ -delayed fission

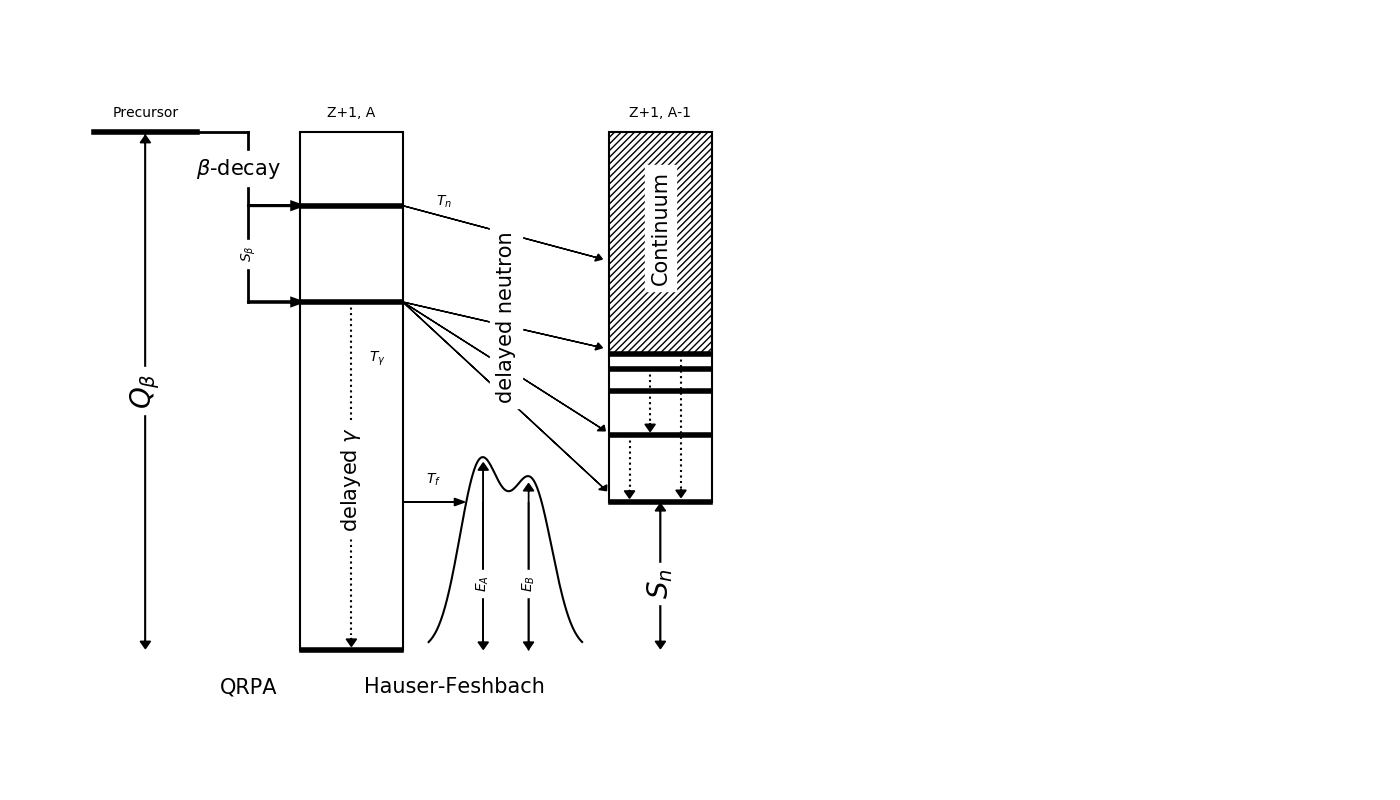
We have recently extended our QRPA+HF model to describe $\beta$ -delayed fission ( $\beta$ df)

Barrier heights from Möller et al. PRC 91 024310 (2015)

Assumes a Hill-Wheeler form for fission transmission

Mumpower et al. PRC 94 064317 (2016) • Spyrou et al. PRL (2016) • Möller et al. ADNDT 125 (2019)
Yokoyama et al. PRC (2019) • Mumpower et al. ApJ (2018)

Multi-chance $\beta$ df

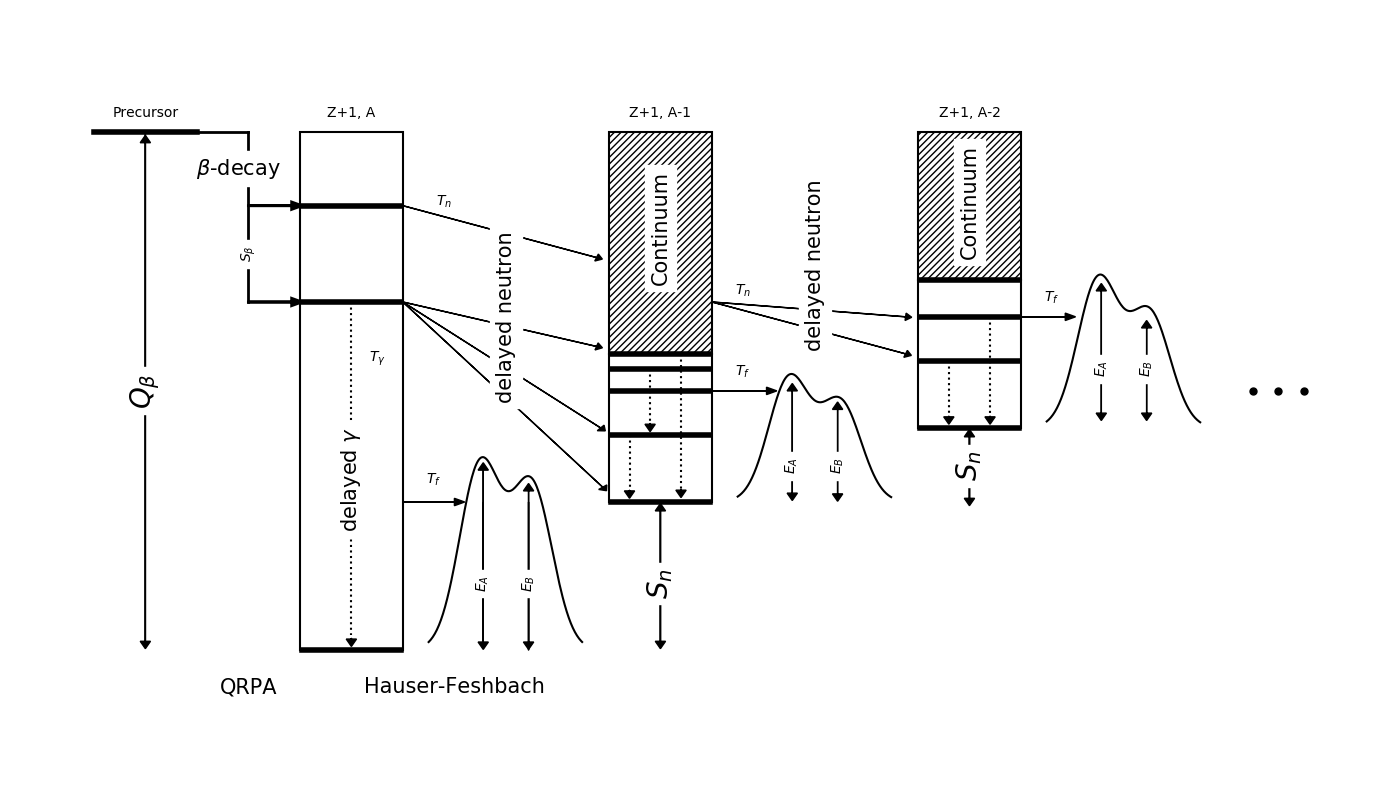
Recall: Near the dripline $Q_{beta}$ ⇡ $S_{n}$ ⇣

Multi-chance $\beta$ df: each daughter may fission

The yields in this decay mode are a convolution of many fission yields!

Mumpower et al. PRC 94 064317 (2016) • Spyrou et al. PRL (2016) • Möller et al. ADNDT 125 (2019)
Yokoyama et al. PRC (2019) • Mumpower et al. ApJ (2018)

Cumulative $\beta$ df probability

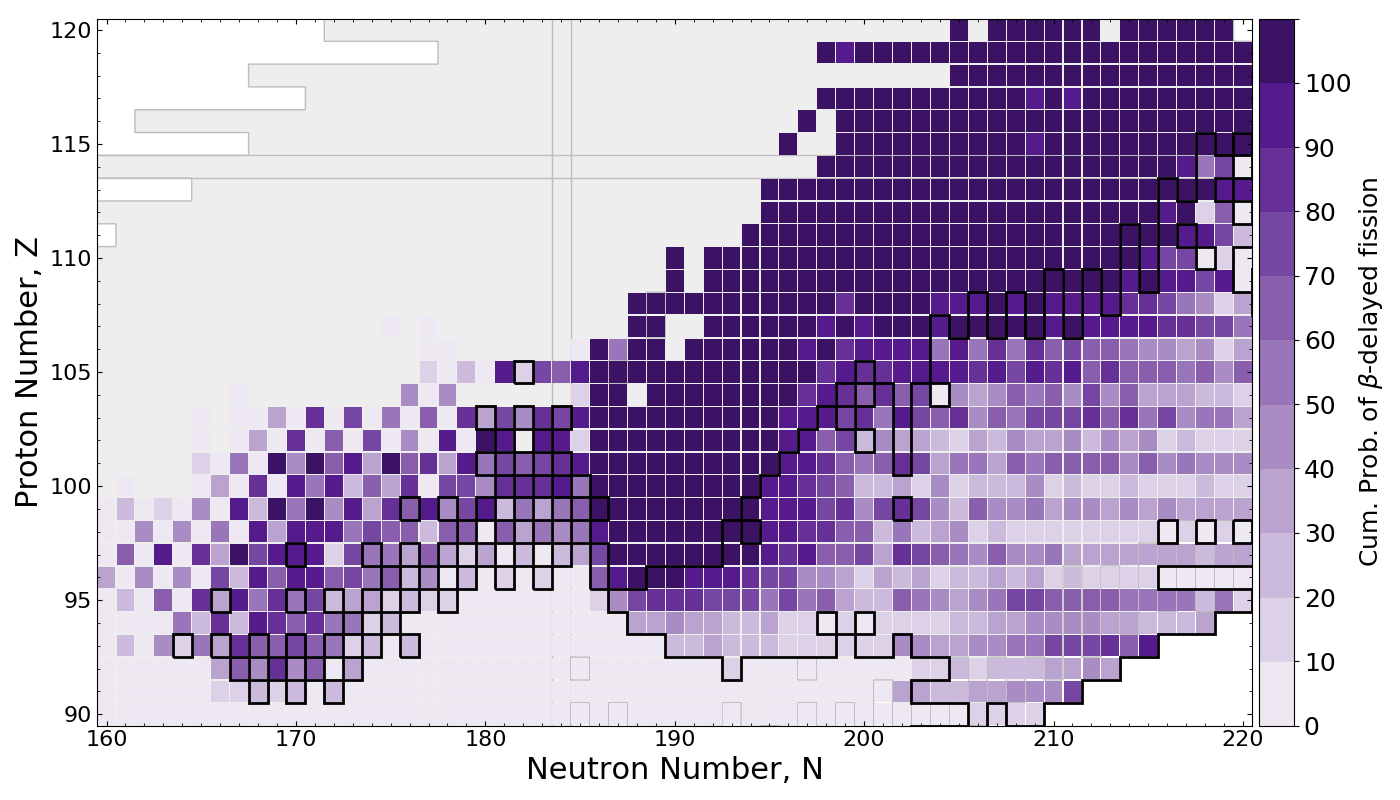
$\beta$ df occupies a large amount of real estate in the NZ-plane

Multi-chance $\beta$ df outlined in black

Mumpower et al. ApJ 869 1 (2018)

Multi-chance $\beta$ df contribution

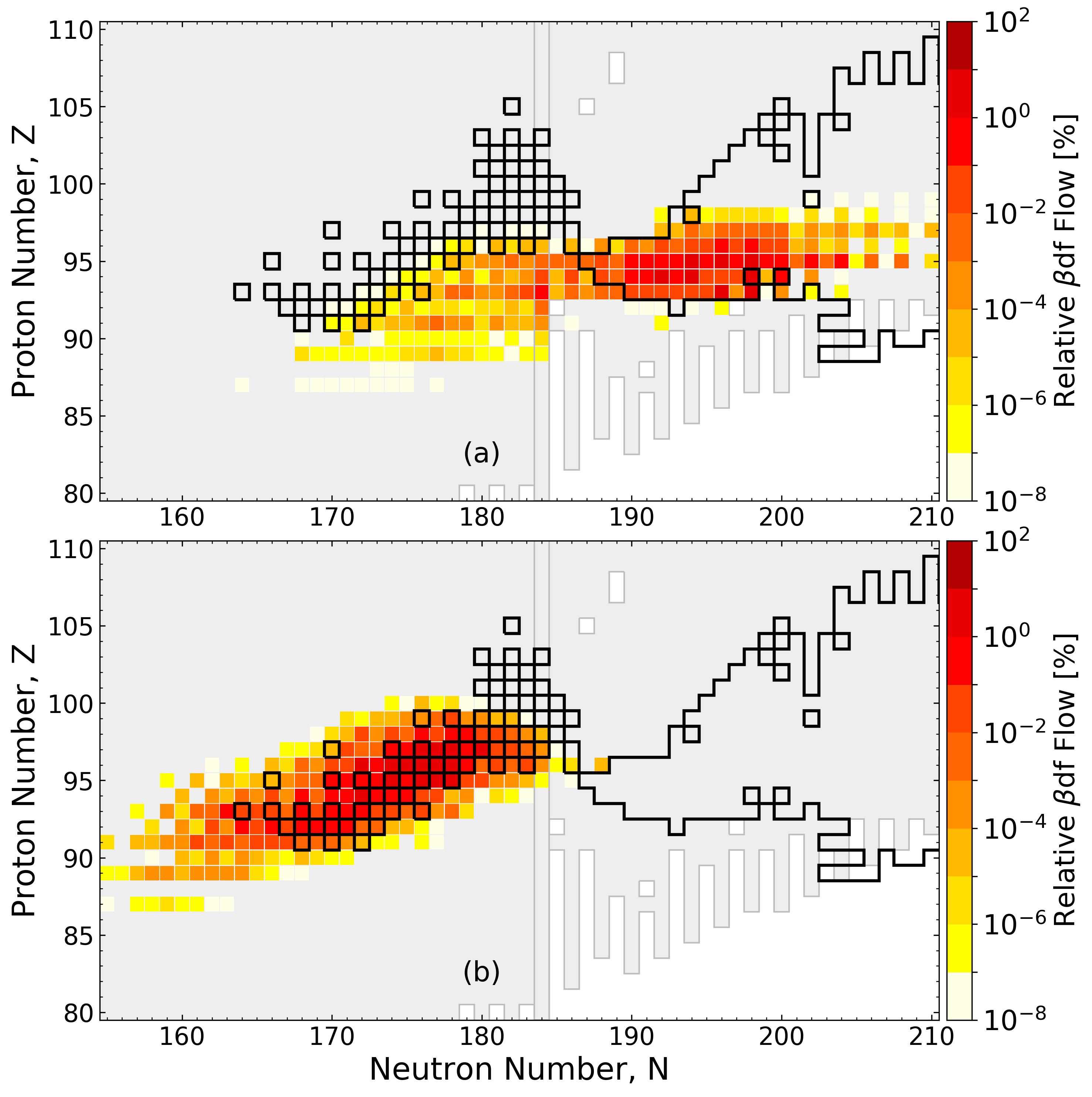
Network calculation of neutron star merger ejecta; FRDM2012 inputs

Multi-chance $\beta$ df contributes at both early and late times

Mumpower et al. ApJ 869 1 (2018)

Application to the $r$ -process

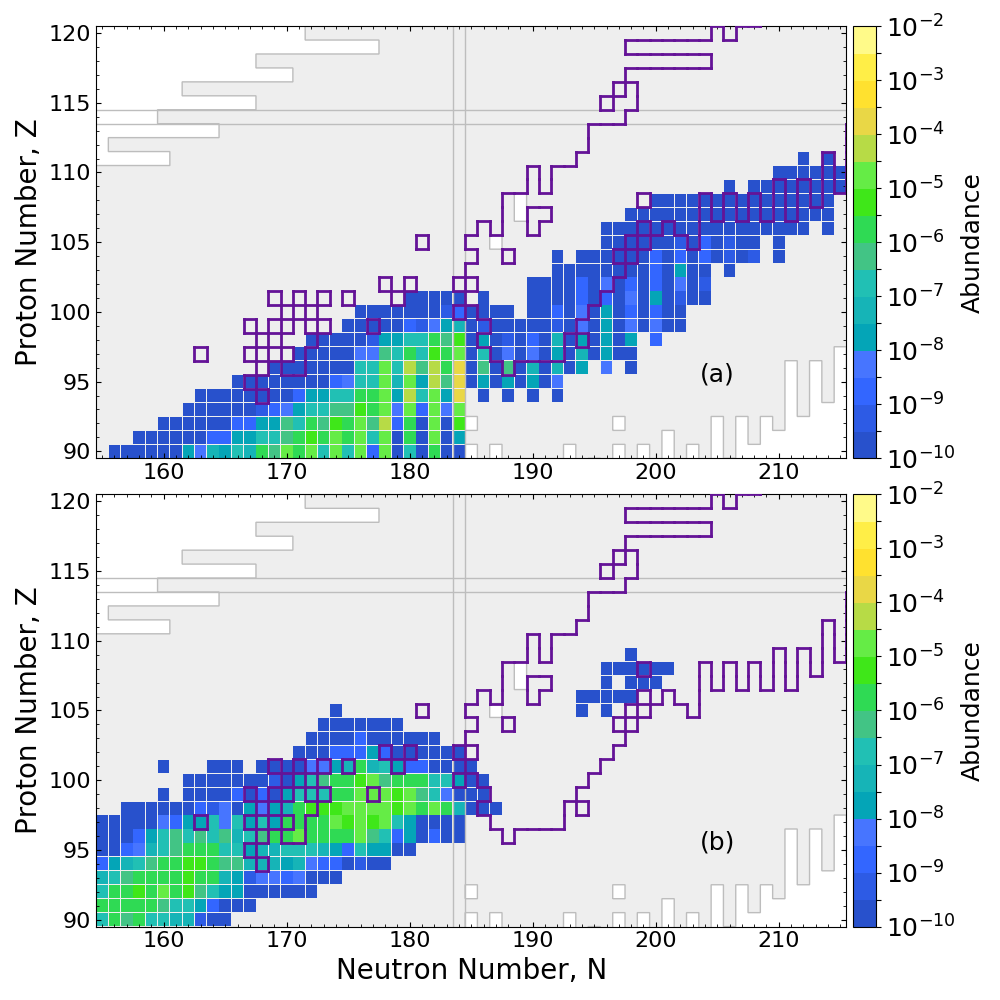
PRISM network calculation of neutron star merger ejecta

$\beta$ df alone may prevent the production of superheavy elements in nature

Thielemann et al. Zeitschrift fur Physik A Atoms and Nuclei 309 4 (1983) • Mumpower et al. ApJ 869 1 (2018)

Impact on final abundances

Network calculation of tidal ejecta from a neutron star merger (FRDM2012)

can shape the final pattern near the $A=130$ peak

This is because of a relatively long fission timescale

Conclusion ⇒ we need a good description of fission yields to understand abundances near $A\sim130$ .

Kodama & Takahashi (1975) • Shibagaki et al. ApJ (2016) • Mumpower et al. ApJ 869 1 (2018) • Vassh et al. J. Phys. G (2019)

fission yields

A simple picture of fission

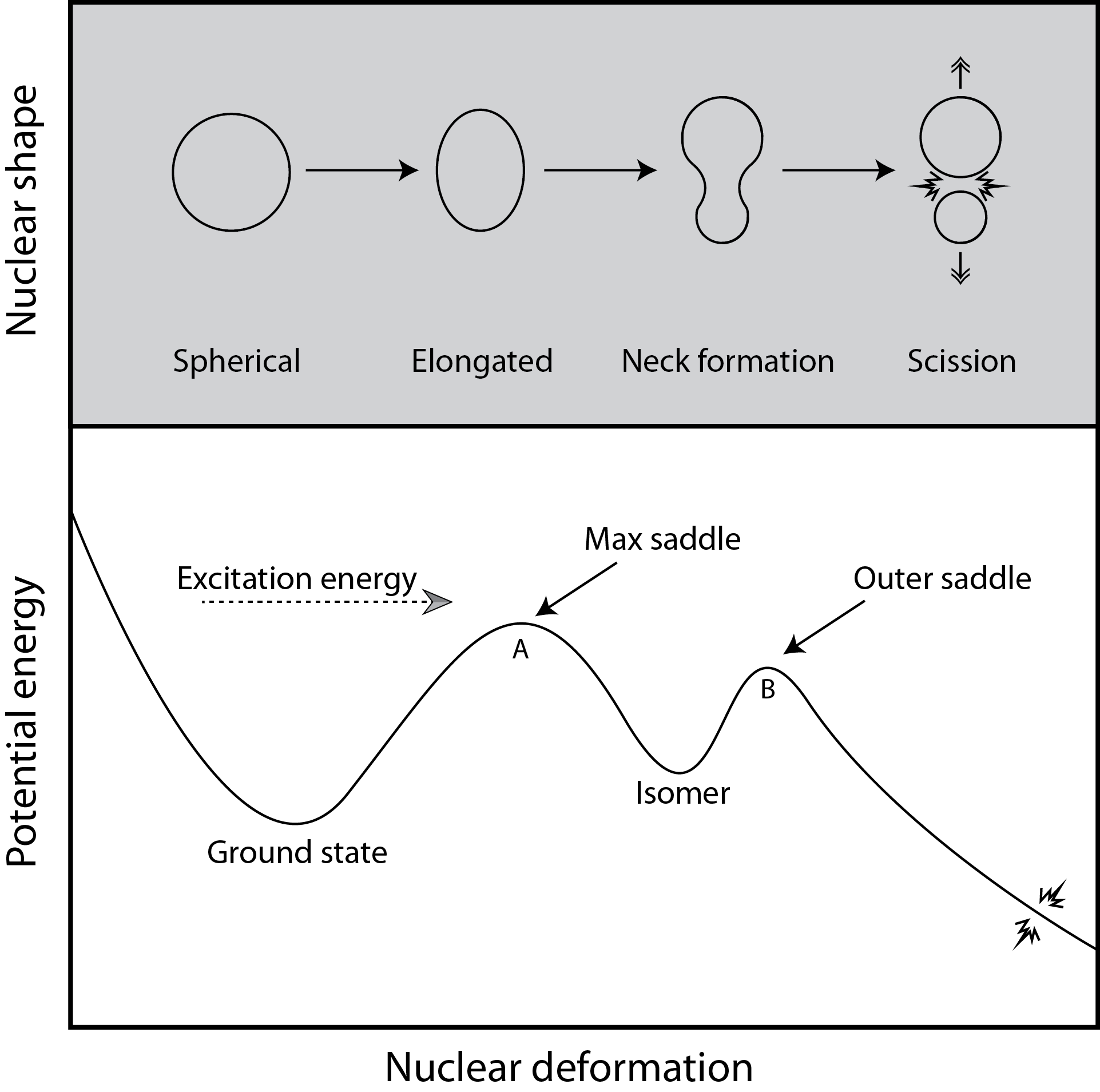
Follow progression of the nucleus from compact to highly elongated shapes

Mumpower et al. in prep. (2019)

Finite-Range Liquid-Drop Model

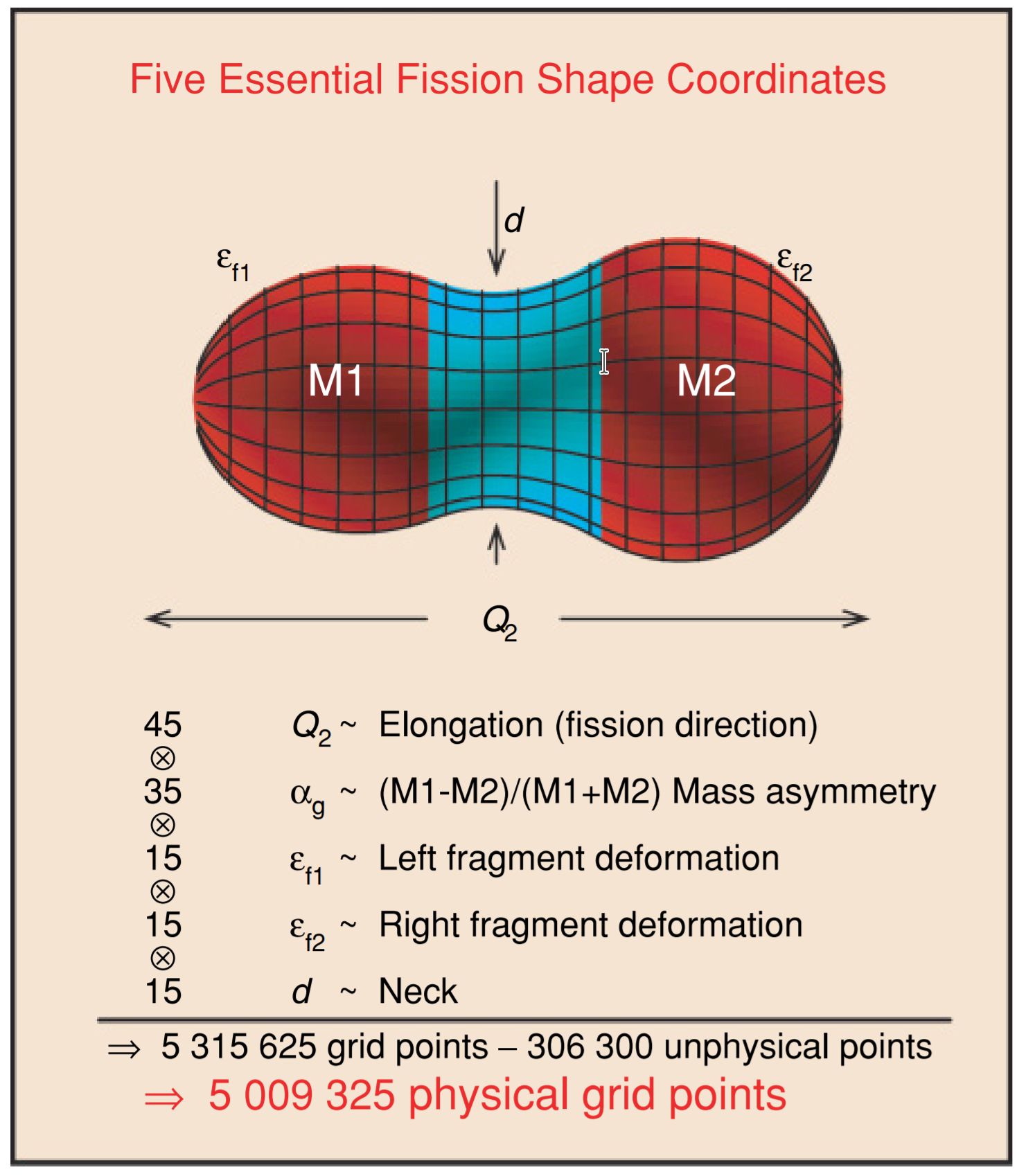
Many possible shape degrees of freedom - but we have to isolate the most important

Möller et al. PRC (2009) • Möller et al. PRC (2015)

How do we calculate fragment yields with this model?

Change in nuclear shape acts as a driving force for bulk rearrangement of material

This results in a collective kinetic energy

The macroscopic shape degrees of freedom couple to individual nucleonic motion

Resulting in an evolution that is both damped and diffuse

This can be approximated as Brownian shape motion

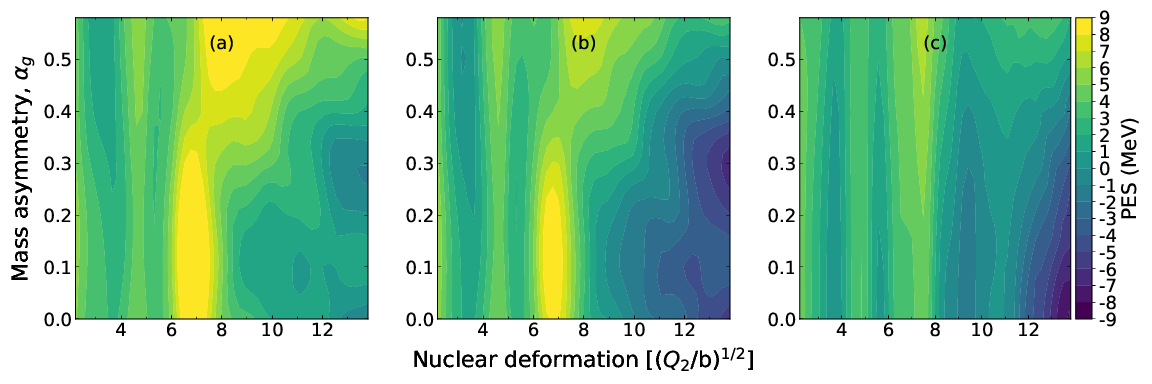
Randrup et al. PRL (2011) • Randrup et al. PRC (2011) • Randrup et al. PRC (2013) • Möller et al. PRC (2015)

Fission evolution

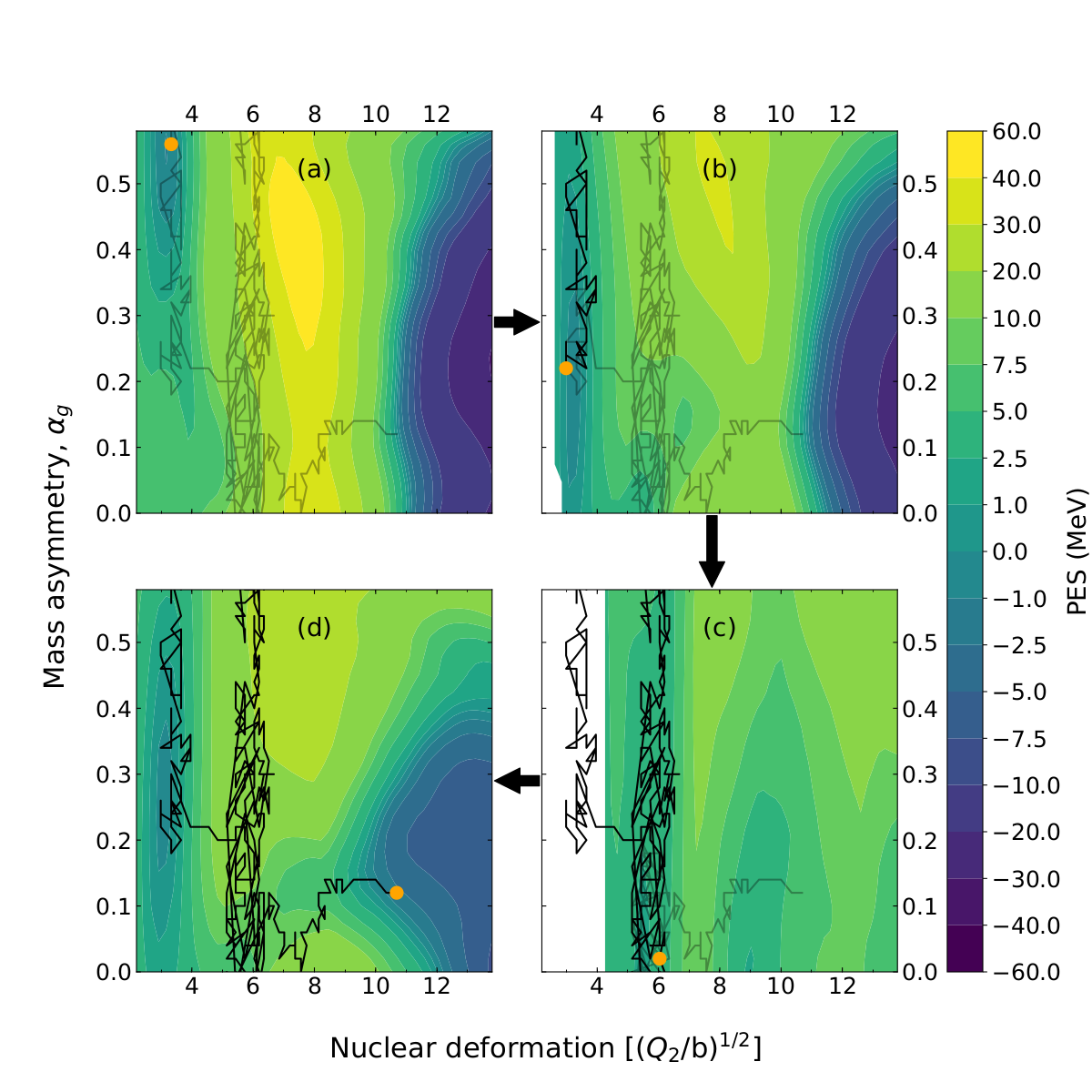
Amounts to random walk across potential energy surface

Mumpower et al. in prep. (2019)

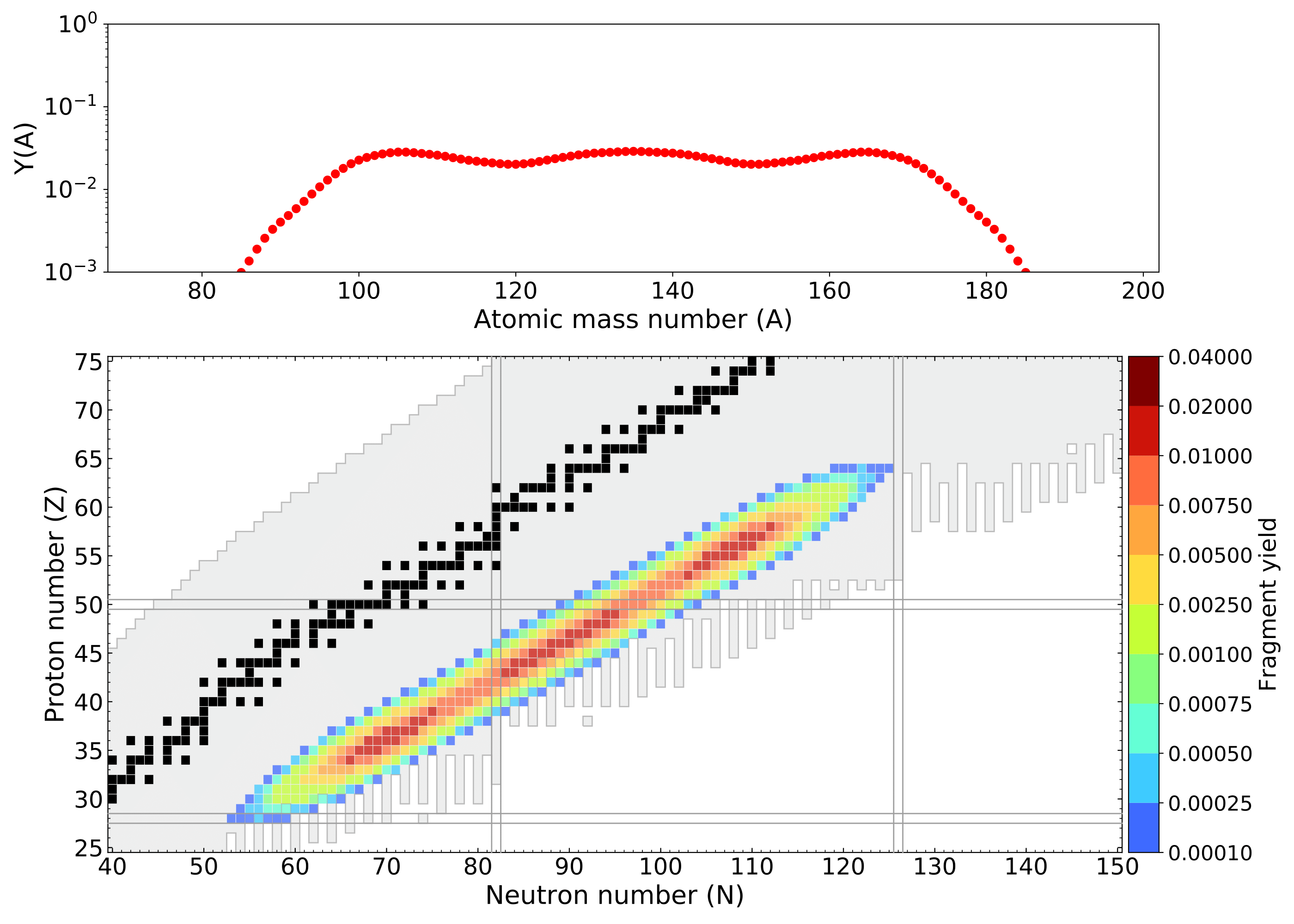
236-U Y(Z,A) yield

Mumpower et al. in prep. (2019)

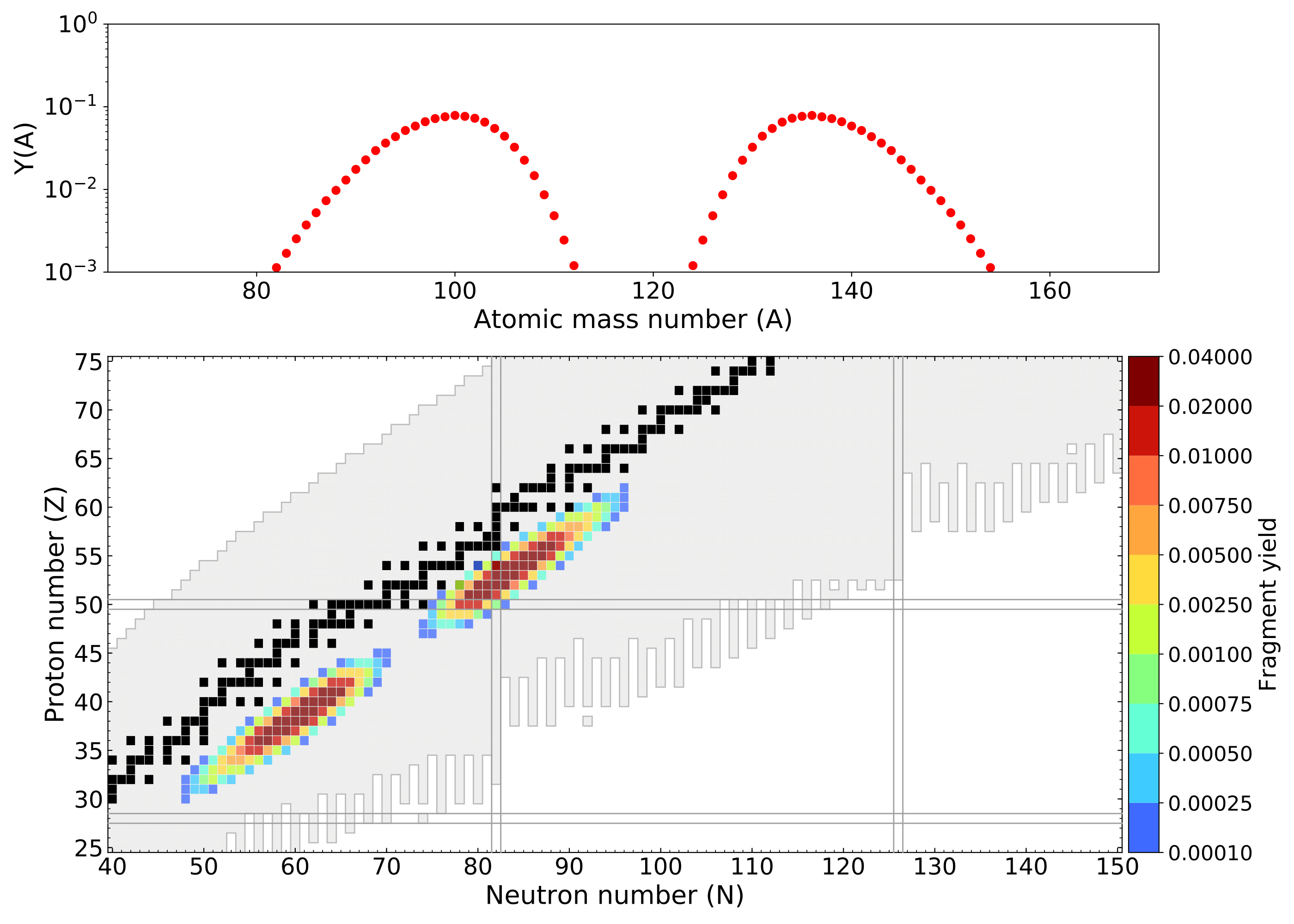
250-U Y(Z,A) yield

Mumpower et al. in prep. (2019)

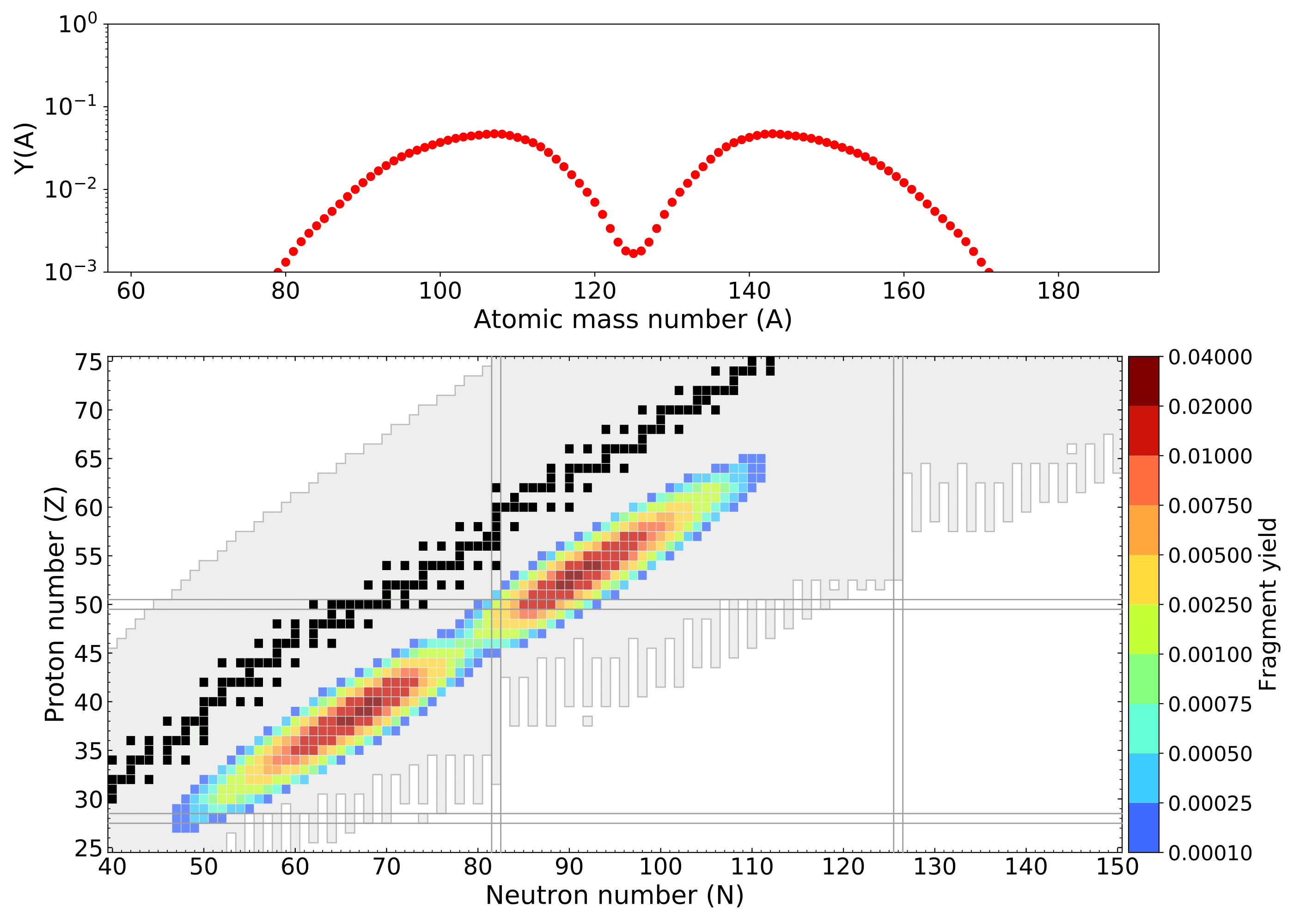
260-U Y(Z,A) yield

Mumpower et al. in prep. (2019)

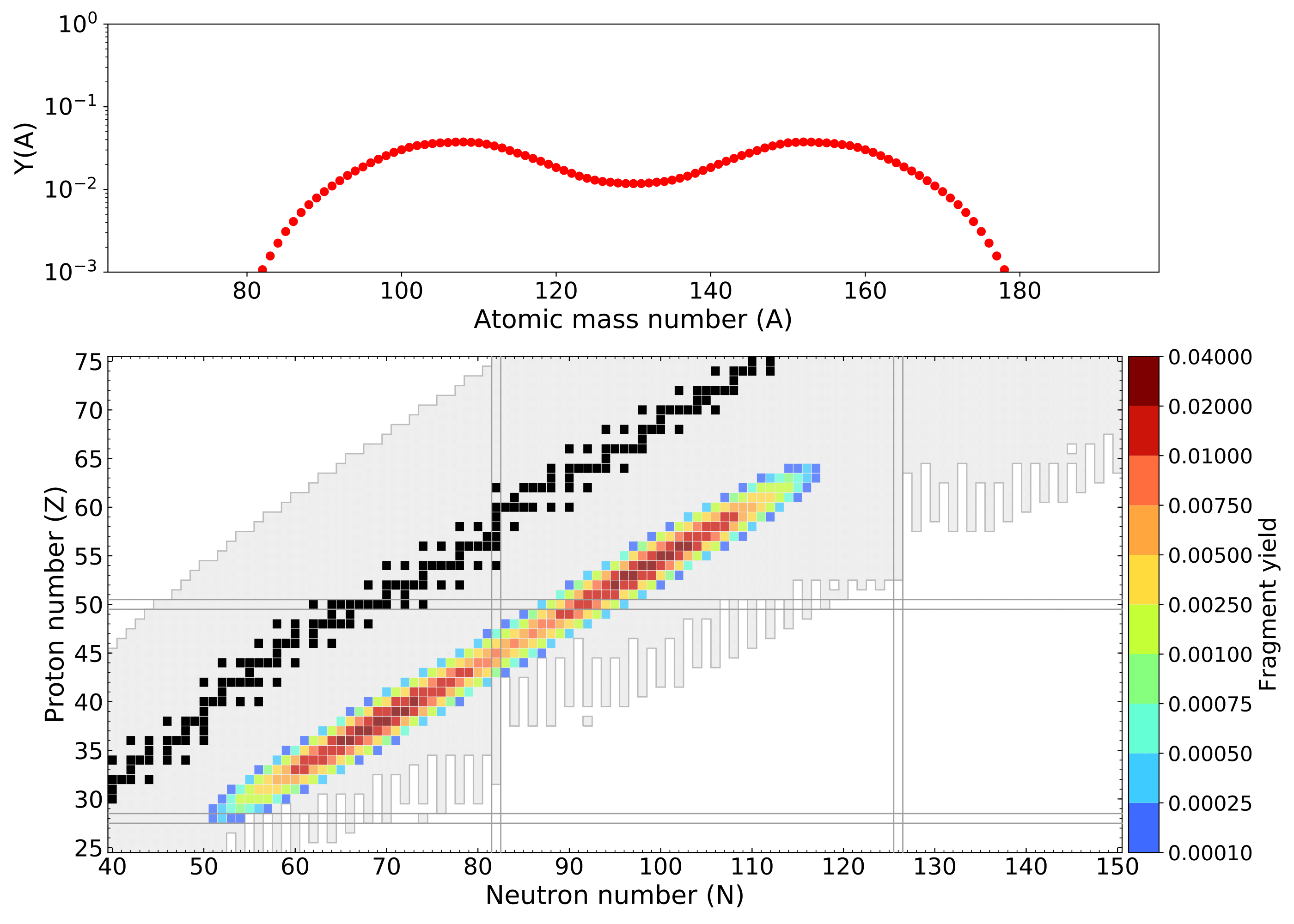
270-U Y(Z,A) yield

Mumpower et al. in prep. (2019)

Number of Peaks

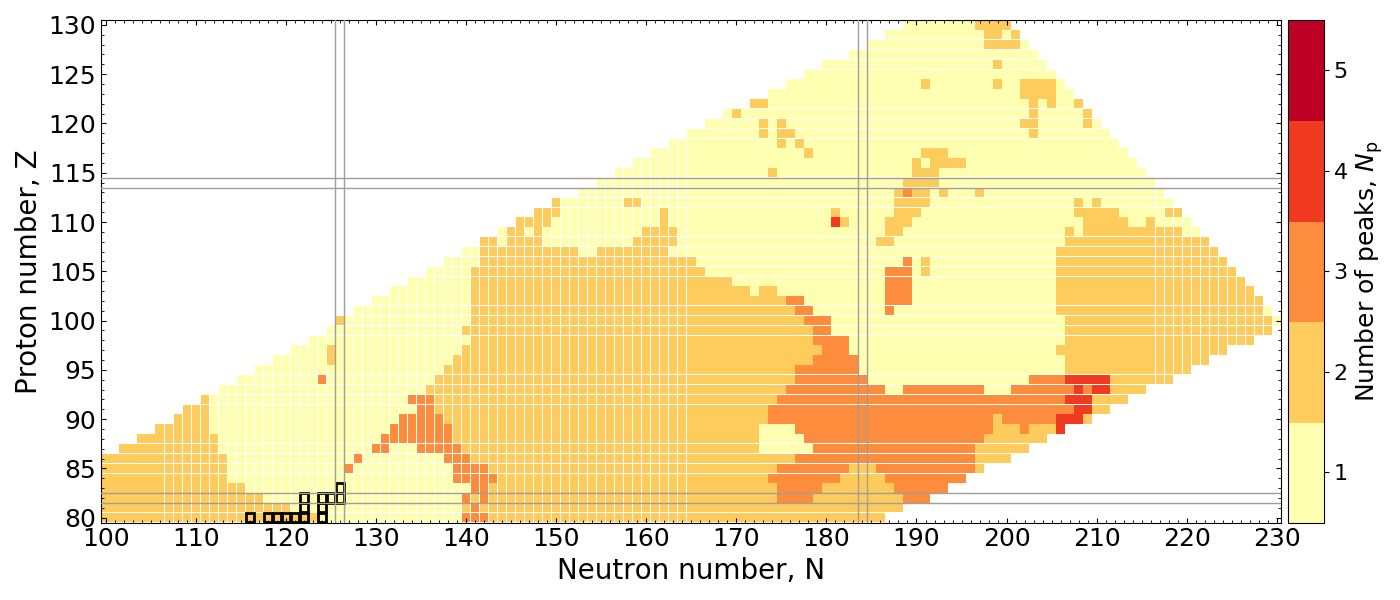
Count the number of peaks in the mass yield, $Y(A)$ , distribution

Rather smooth variation in number of peaks across chart of nuclides.

$r$ -process region: 2 or 3 peaks are the norm given our prediction of fission hot spots

Mumpower et al. in prep. (2019)

Measure of Asymmetry

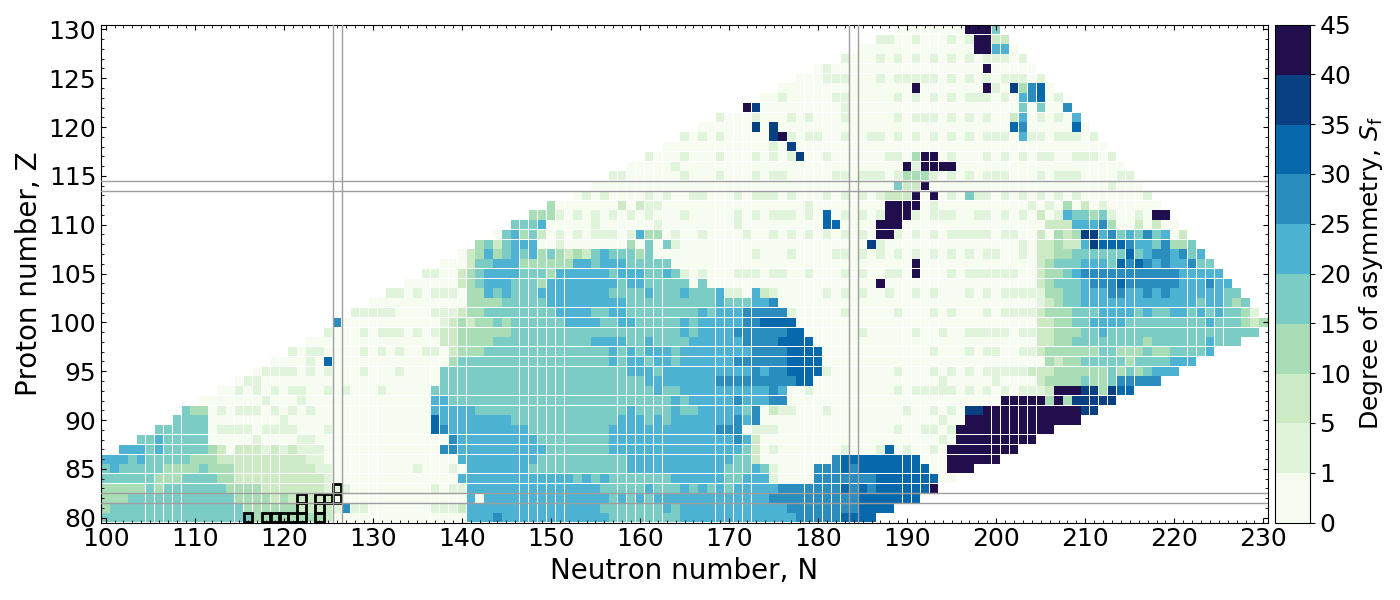
Measure the distance in $A$ between the maxima of $Y(A)$ and $Y(A_{\rm f}/2)$

Abrupt changes can be seen when the maxima shift from symmetric to asymmetric

Symmetric followed by asymmetric distributions can be expected in $r$ -process simulations

Mumpower et al. in prep. (2019)

Extent of Y(A) Distribution

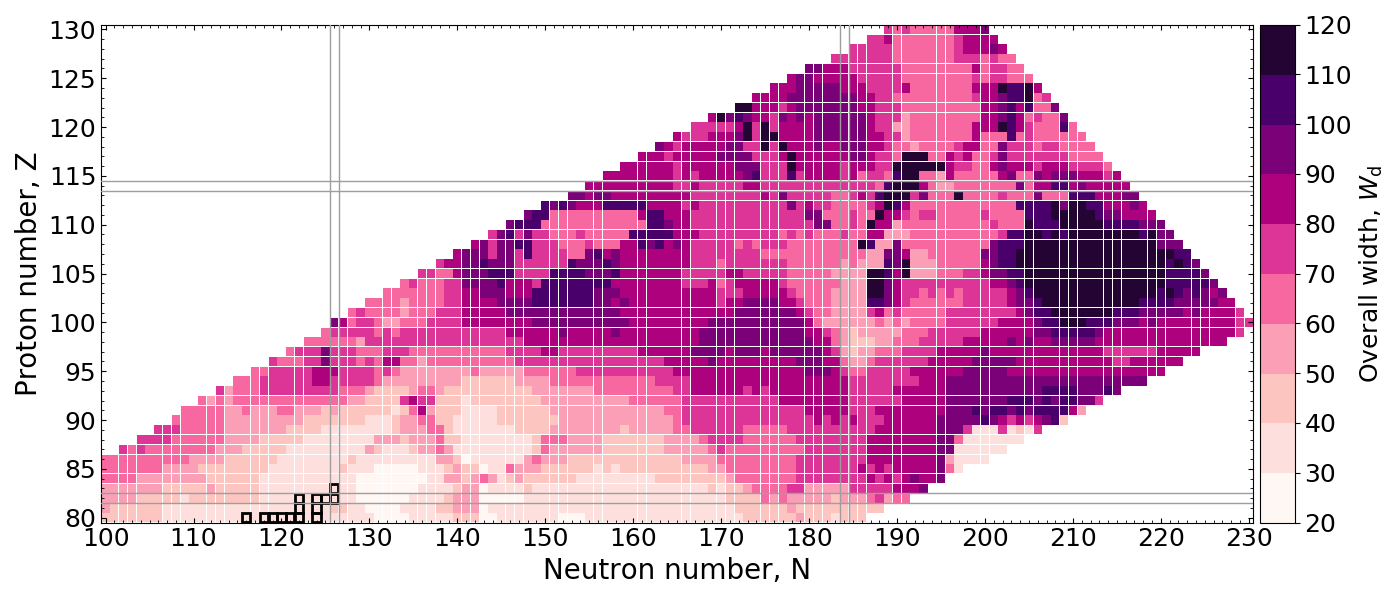
Measure the spread of the daughter products in $A$

Strong dependence can be seen with the fission system

Wiggles in the yield (number of peaks or asymmetry) don't matter if the distribution is wide!

Mumpower et al. in prep. (2019)

Peak Location (A)

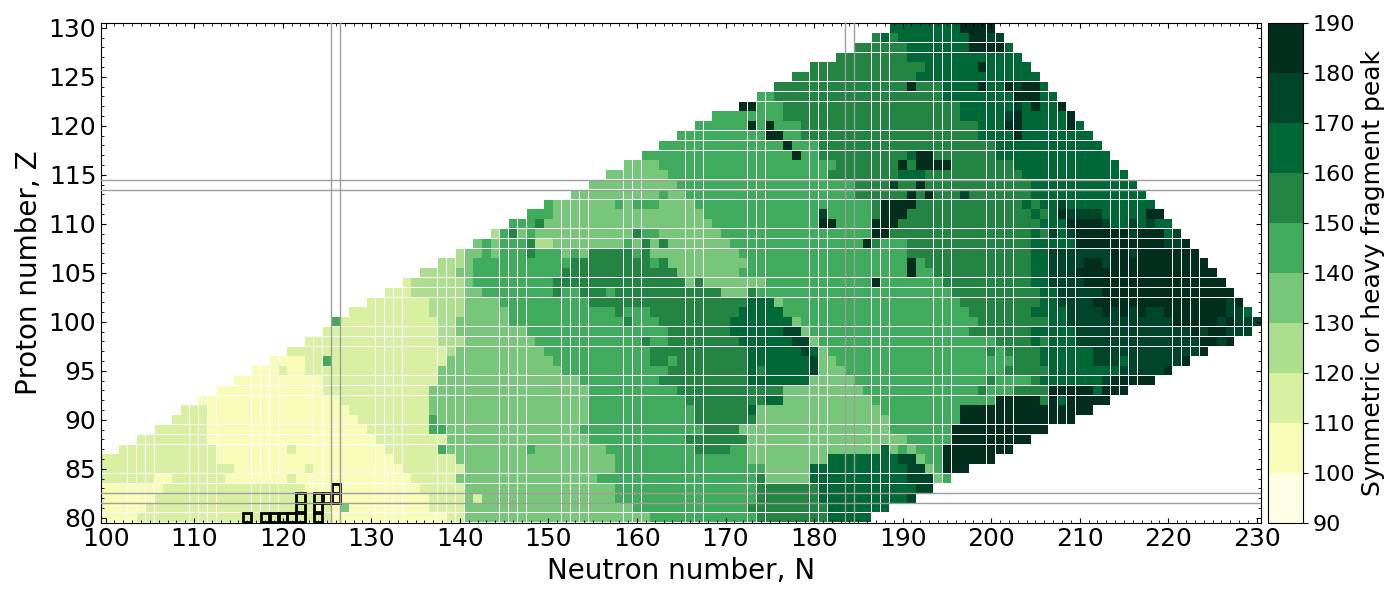
Measure the placement of material of the highest peak in $A$

Notice the transition between 3 and 2 peaks plays an important role

$r$ -process conditions from astro. simulations suggest population of $A\sim150$ to ligher nuclei

Mumpower et al. in prep. (2019)

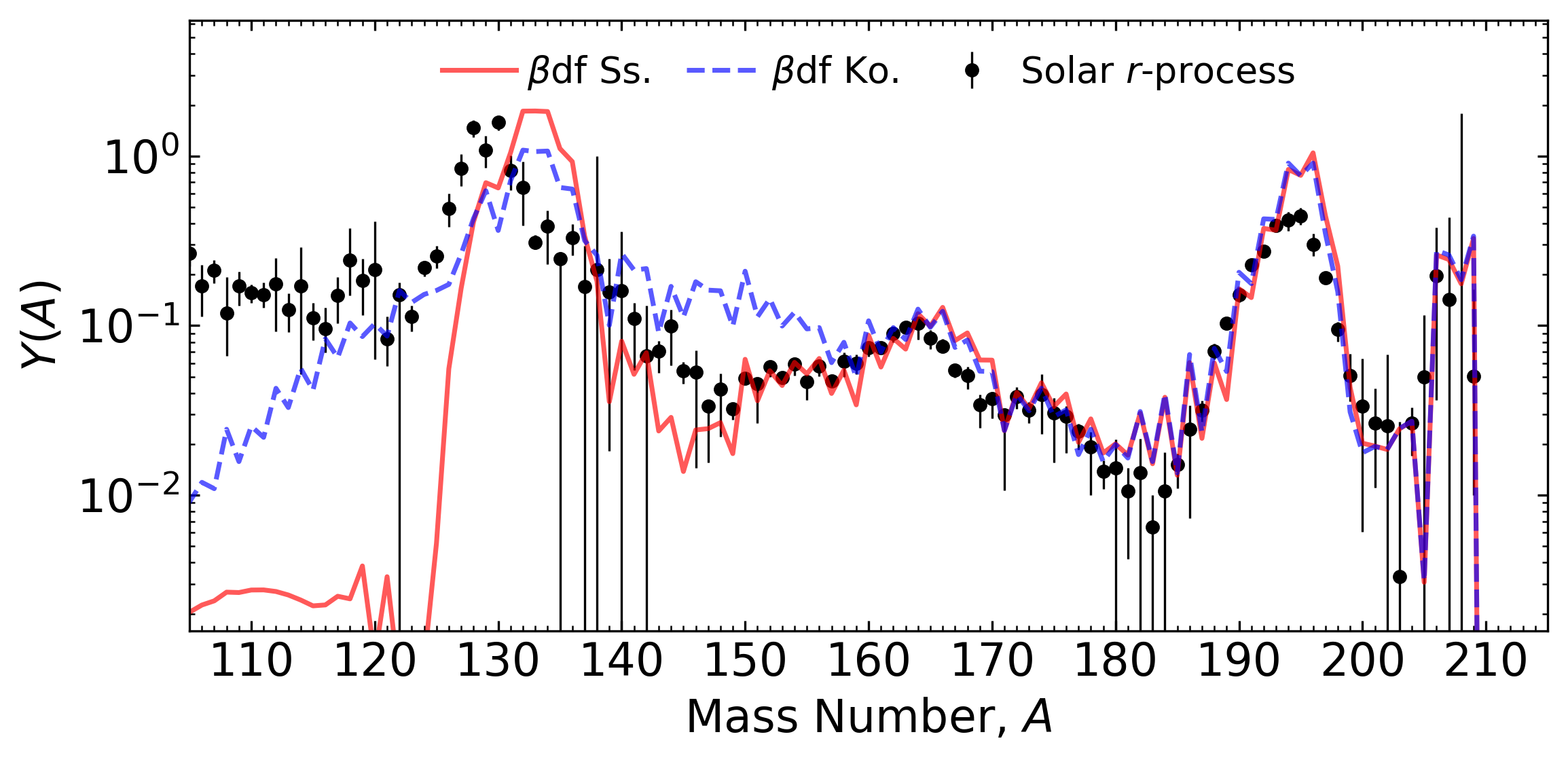
Impact on the abundances

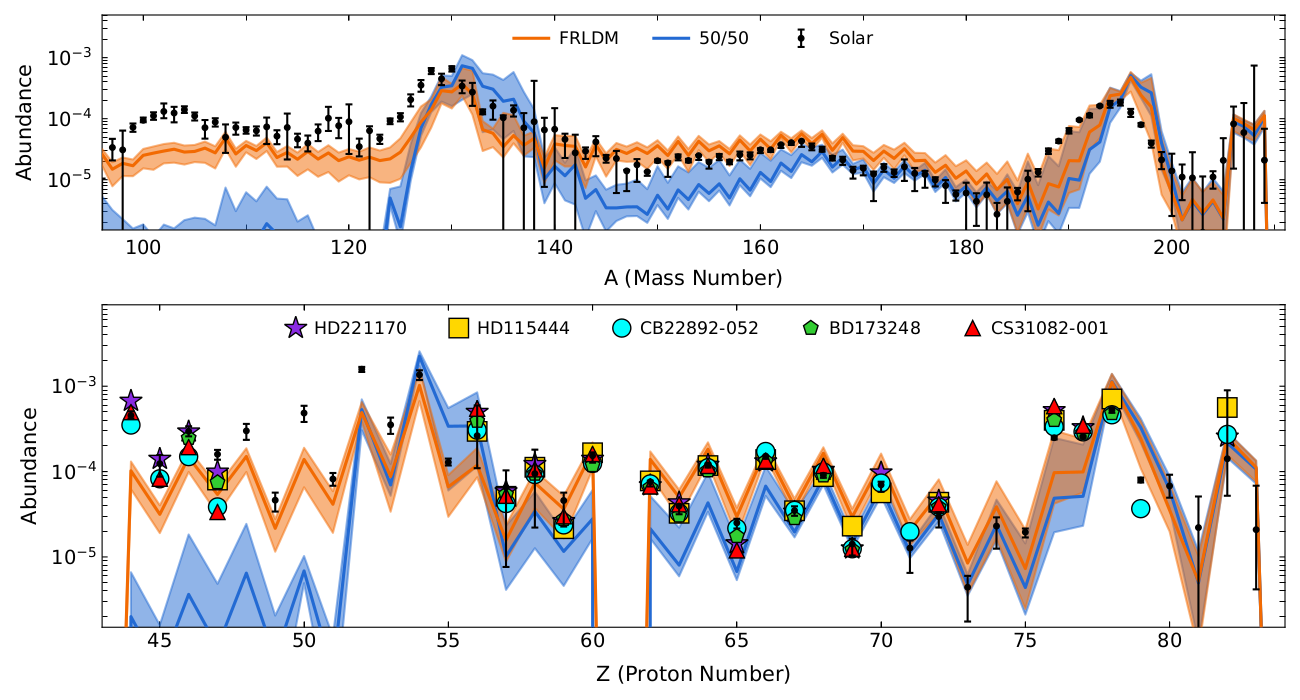
Abundance output using common old nuclear fission data and our new model predictions

Co-production of light nuclei from $Z\sim 45$ to the actinides (dynamical merger ejecta only!)

Universality may extend further down to lighter nuclei than commonly accepted in the literature

Vassh et al. in prep. (2019)

Special thanks to

My collaborators

A. Aprahamian, J. Barnes, A. Burrows, J. Clark, B. Côté, J. Dolance, W. Even, C. Fontes, C. Fryer, E. Holmbeck, A. Hungerford, P. Jaffke, T. Kawano, O. Korobkin, J. Lippuner, G. C. McLaughlin, J. Miller, W. Misch, P. Möller, R. Orford, J. Randrup, G. Savard, T. Sprouse, R. Surman, N. Vassh, M. Verriere, R. Vogt, R. Wollaeger, Y. Zhu
& many more...

▣ Student ▣ Postdoc ▣ CTA Staff ▣ FIRE PI

Summary

The $r$ -process requires a deep understanding of fission

Recent calculations give insight into:

Re-cycling material ▴ Production of heaviest elements ▴ Late-time observations

FRIB, etc. will help to constrain nuclear models, but the heaviest elements will remain relatively inaccessible

We therefore need to keep developing and studying theoretical models of nuclear physics, especially fission

Nuclear modeling is absolutely crucial if we want to prove definitively that heavy elements such as the actinides were made in an event

Results / Data / Papers @ MatthewMumpower.com

What is left after fission?

Long-lived actinides

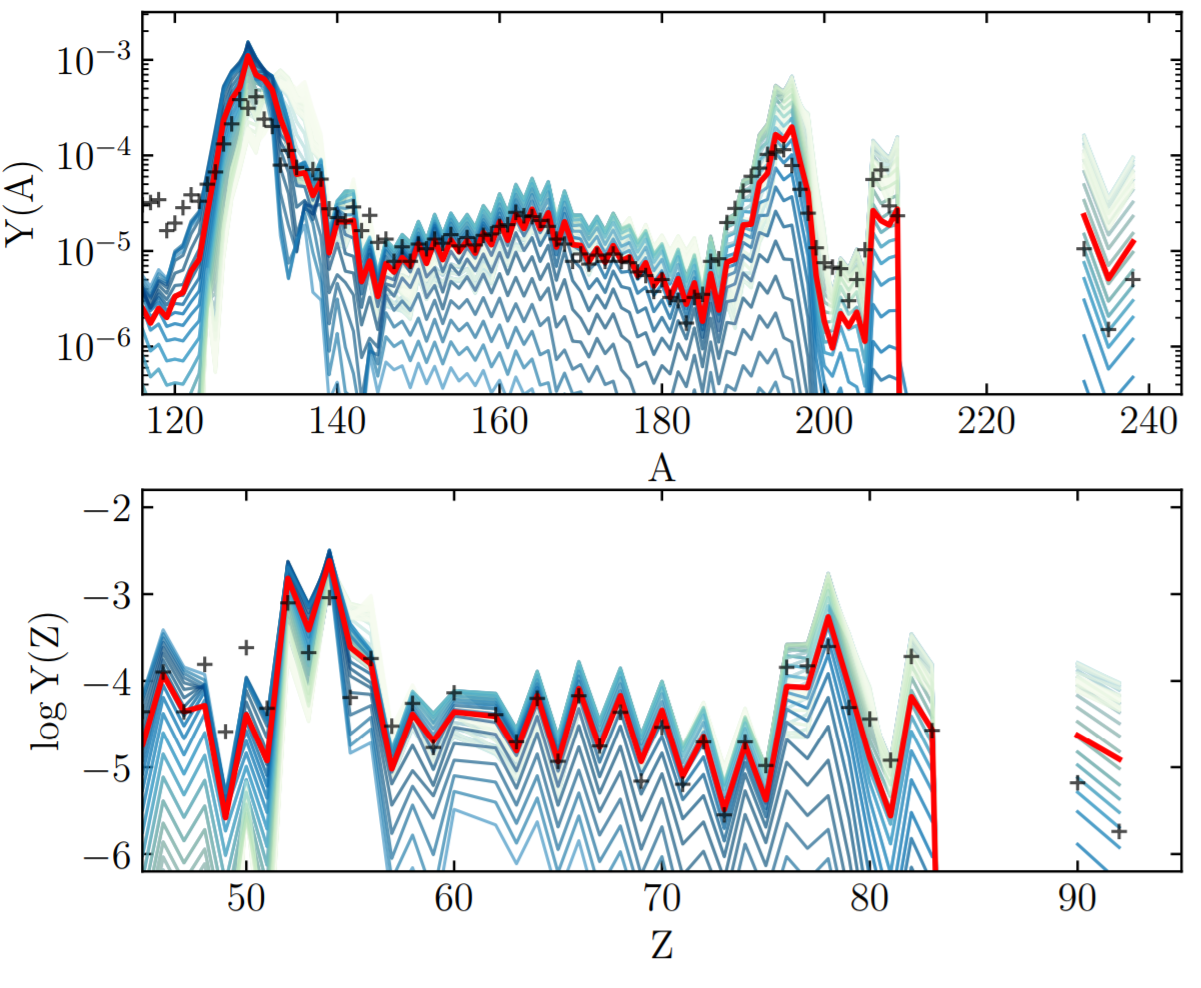
In some simulations actinides seem to be overproduced versus lanthanides

A sufficient amount of with ligher $r$ -process material is required to match the solar isotopic residuals

∴ Fission theory has implications far beyond nucleosynthetic outcomes; e.g. for galactic chemical evolution, etc.

Holmbeck et al. ApJ 870 1 (2019) • Vassh et al. J. Phys. G (2019)

One example: $^{254}$ Cf(Z=98)

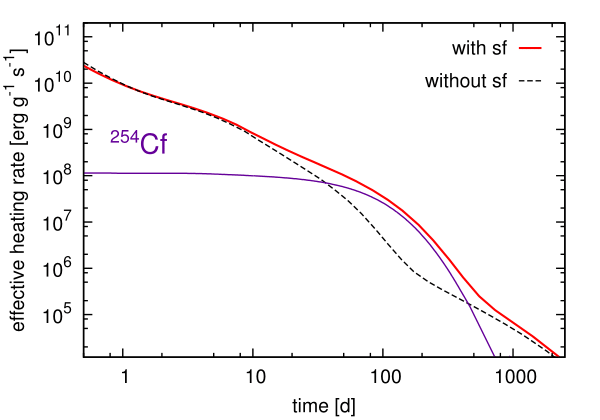
Is there any possible precursor to show that actinide nucleosynthesis has occurred in an event?... Maybe!

The spontaneous fission of $^{254}$ Cf can be a primary contributor to nuclear heating at late-time epochs

The $T_{1/2}\sim 60$ days; found from nuclear weapons testing

Baade et al. PASP (1956) • Conway et al. JOSA (1962) • Wanajo et al. ApJL (2014) • Y. Zhu et al. ApJL 863 2 (2018)
Vassh et al. J. Phys. G (2019)

Production of $^{254}$ Cf(Z=98)

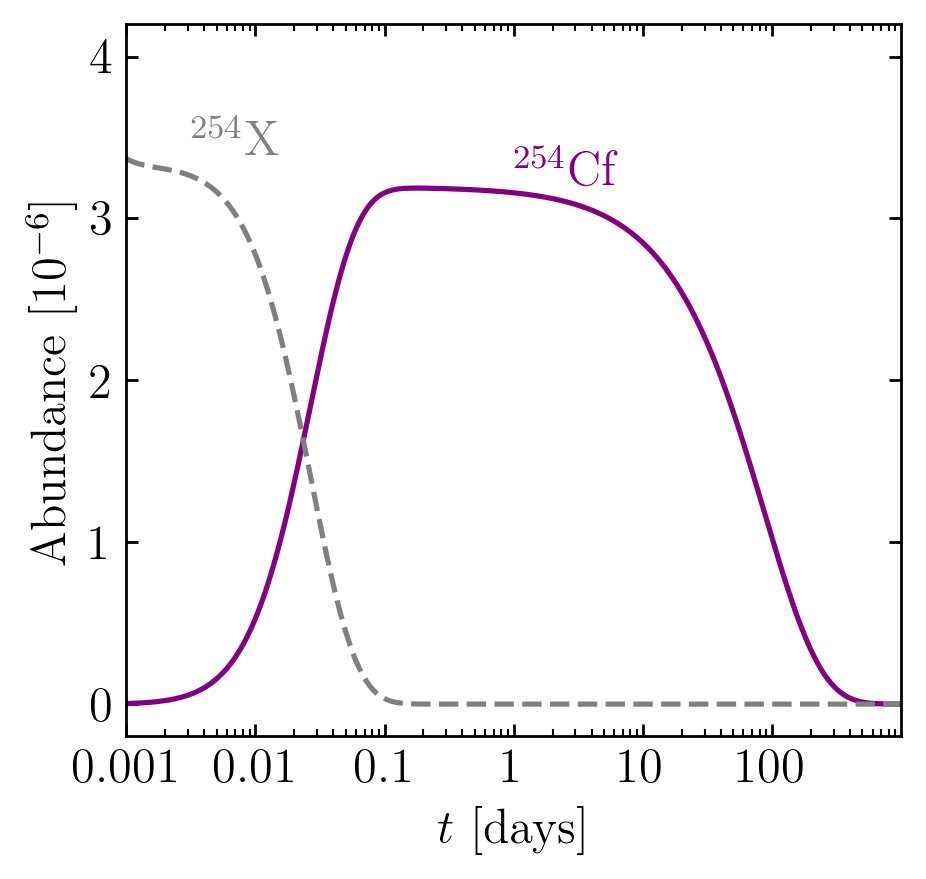
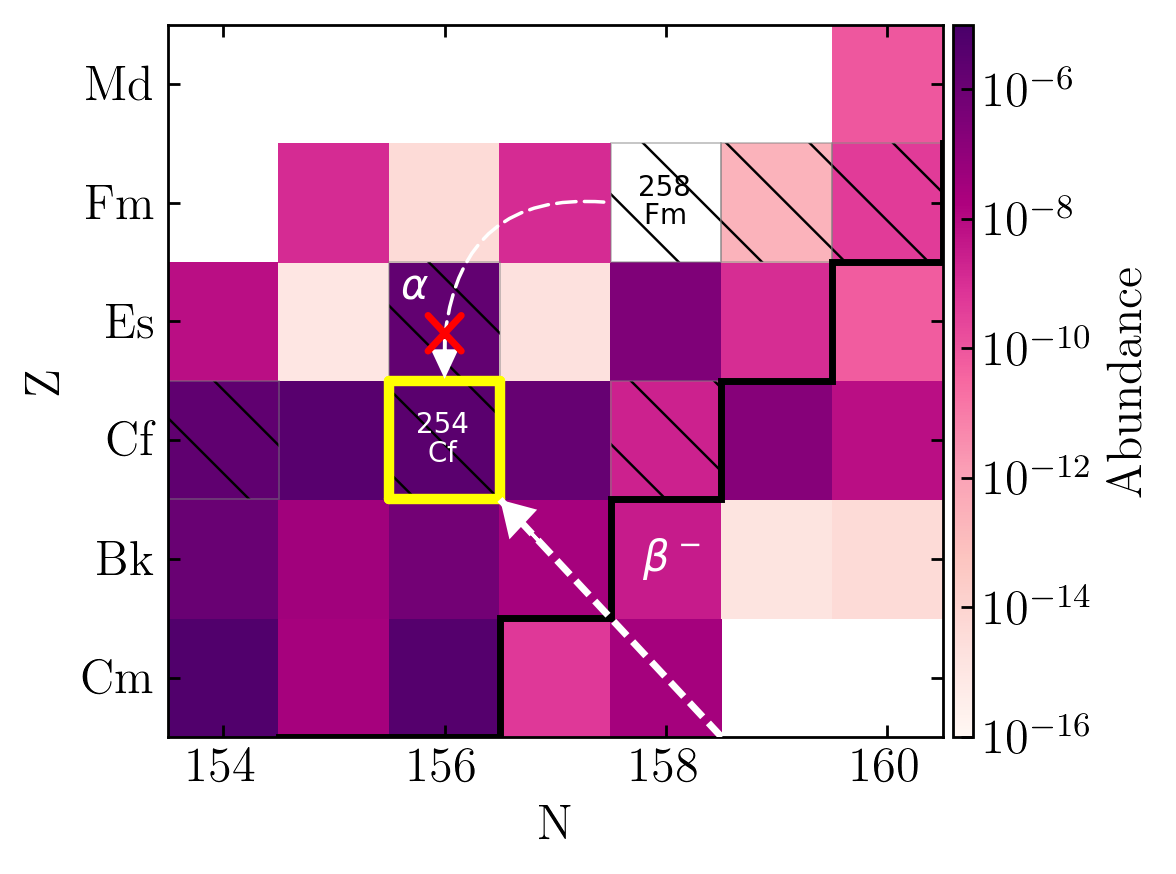
Primary feeder seems to be from $\beta$ -decay

Production of this nucleus been explored over a range of nuclear models; some high - some low

Remains to be seen if we can disentangle from other late-time heating sources (e.g. puslar or accreetion fallback)

Wanajo et al. (2014) • Y. Zhu et al. ApJL 863 2 (2018) • Vassh et al. J. Phys. G (2019) • Wollaeger et al. ApJ (2019) • Wu et al. PRL (2019)

Observational Impact of Californium

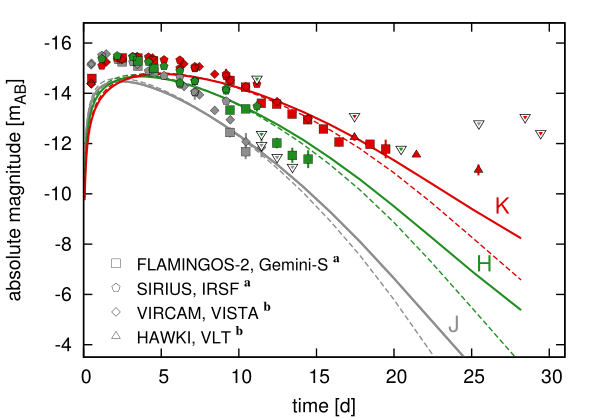
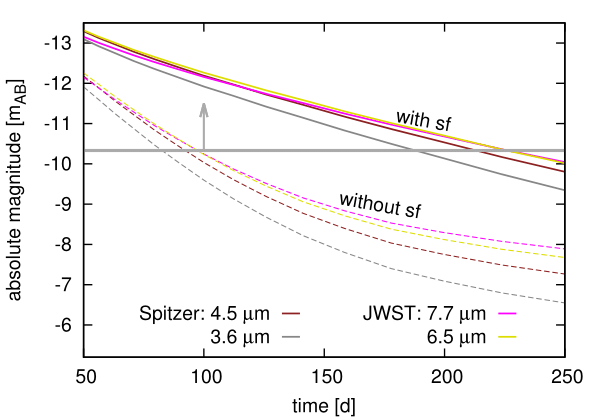
Both near- and middle- IR are impacted by the presence of $^{254}$ Cf

Late-time epoch brightness can be used as a proxy for actinide nucleosynthesis

Future JWST will be detectable out to 250 days with the presence of $^{254}$ Cf

This also has implications for merger morphology...

Wanajo et al. (2014) • Y. Zhu et al. ApJL 863 2 (2018) • Vassh et al. J. Phys. G (2019) • Wollaeger et al. ApJ (2019) • Wu et al. PRL (2019)

Fission across the chart of nuclides and implications for the rr-process

Matthew Mumpower

Fission across the chart of nuclides
and implications for the $r$ -process