The Los Alamos fission yield evaluation pipeline

        LA-UR-19-29974

Matthew Mumpower

FPY workshop

Thursday Oct. 3$^{rd}$ 2019

Nuclear Data Team
Theoretical Division

Outline

• Motivation
• What is an evaluation?
• Progress on our evaluation pipeline
• Summary

Why do we need fission yields?

Fission yields are needed for a variety of applications

Industrial applications: simulation of reactors, fuel cycles, waste management

Experiments: backgrounds, isotope production with radioactive ion beams (fragmentation)

Science applications: nucleosynthesis, light curve observations

Other Applications: national security, nonproliferation, nuclear forensics

What is a fission yield evaluation?

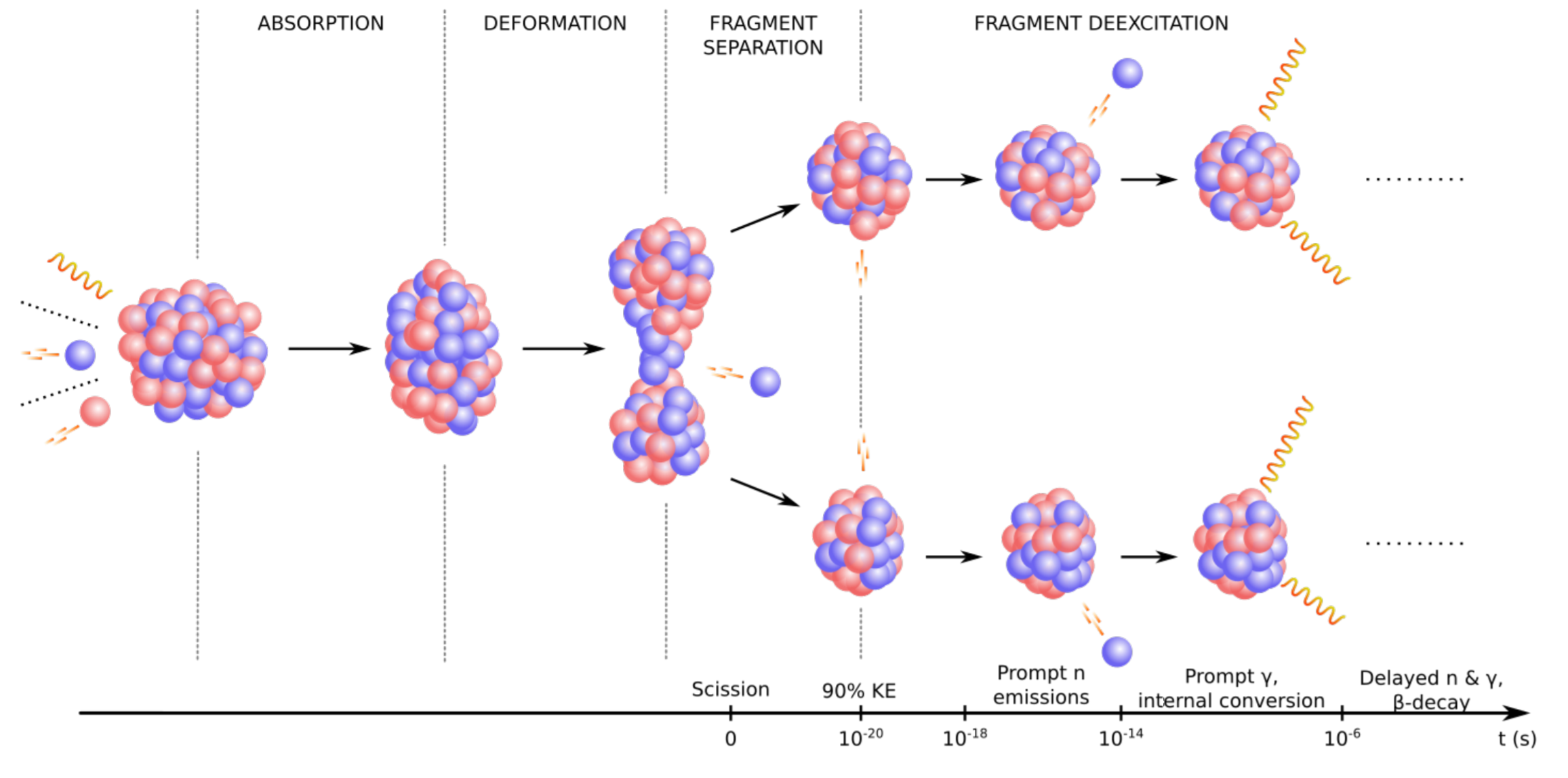
An evaluation combines experimental and theoretical knowledge consistent with physical laws

to produce a quantity (in this case fission yields) with verifiable quality.

Should be distributed in an easily accessible form that all case use (e.g. ENDF or GNDS)

for a variety of applications

Theory is limited in accuracy & measured data is limited in scope

Current status of fission yield evaluations

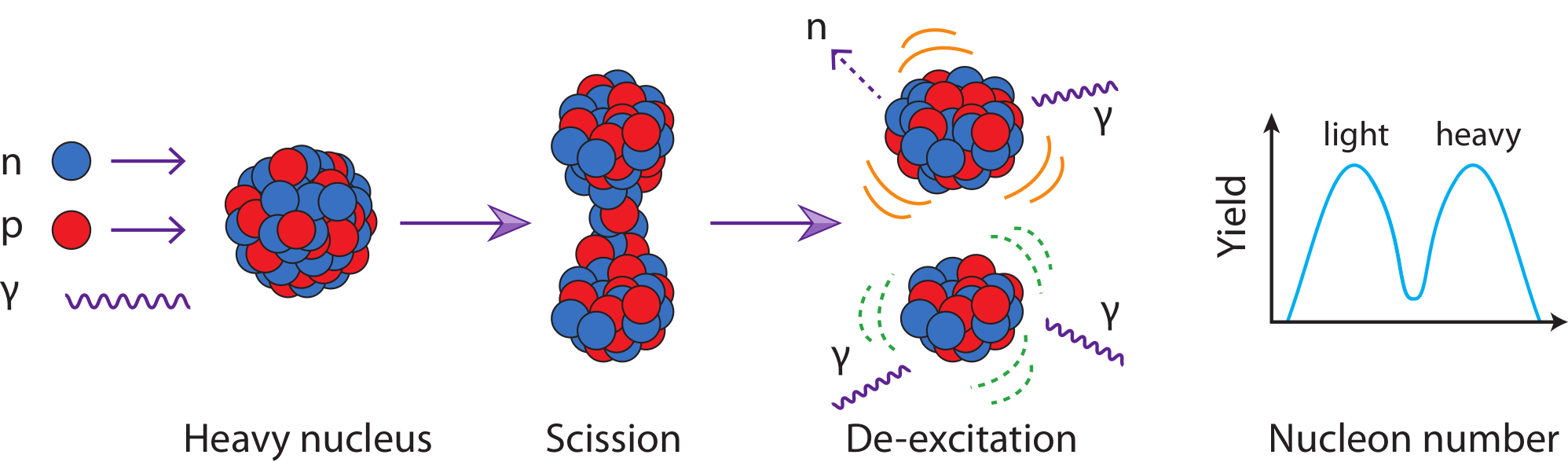
The last update to ENDF fission yield evaluation was in the 1990's

Other evaluations exists such as (JEFF, JENDL, etc.)

We want to improve several key areas:

• improve continuous energy dependent information
• provide consistency between yields, n's & $\gamma$'s and decay data
• more complete uncertainties

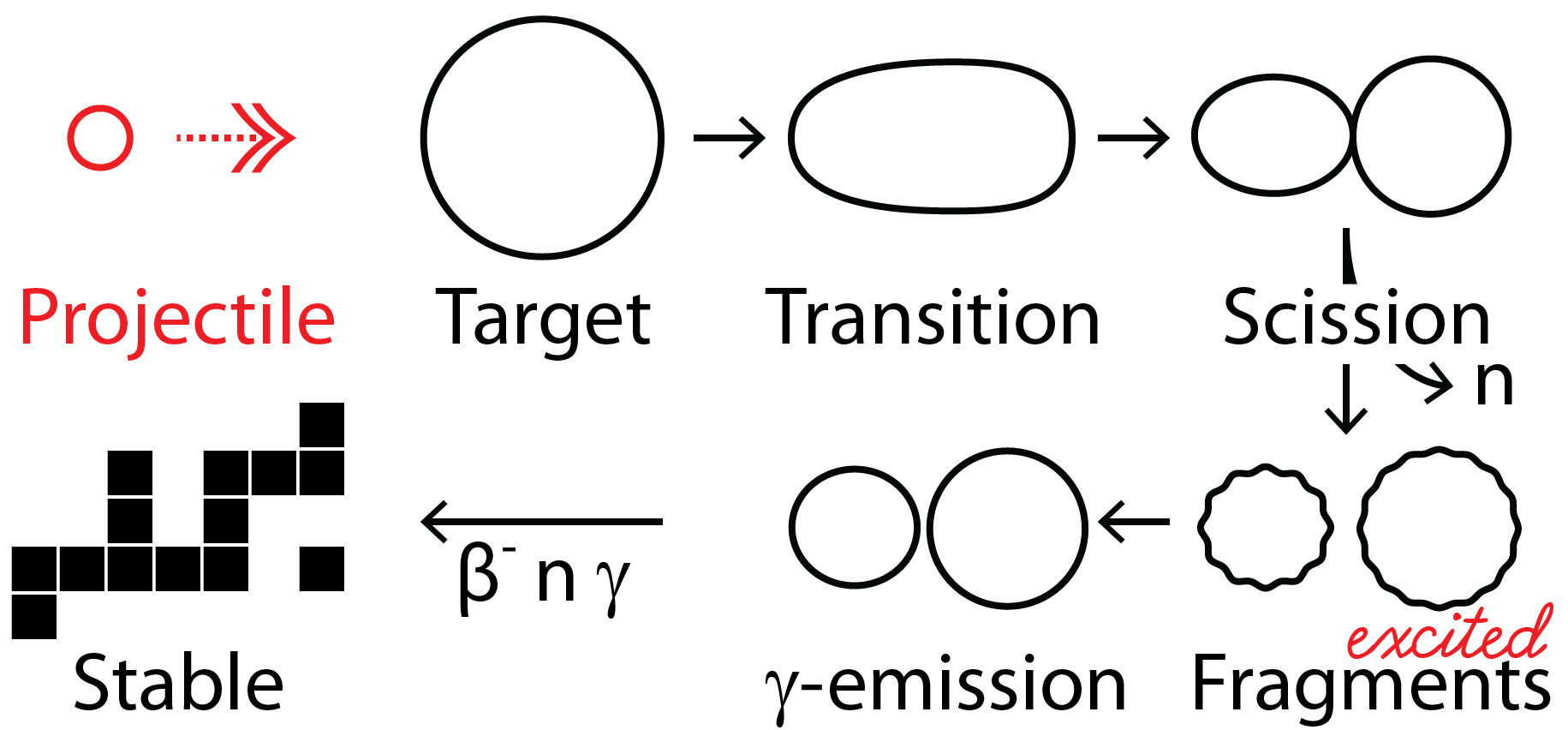
The Los Alamos Fission Yield Evaluation

Purpose: to provide a modern evaluation of fission yields

With a focus on consistency between yields, n's & $\gamma$'s, and decay data

This includes:

• independent yield (after prompt particle emission)
• cumulative yield (after all decays)

We also seek to expand continuous energy dependent information

Auxiliary information:

primary yield (before any prompt particle emission)

Particle spectra and multiplicities (n's & $\gamma$'s)

The LANL Fission Evaluation Pipeline

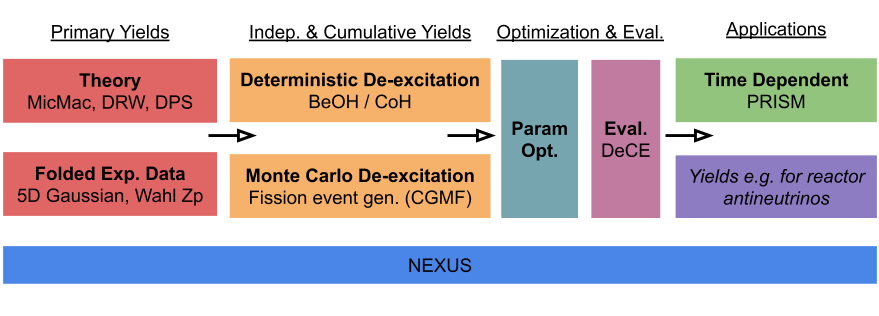
Our current workflow is a combination of many distinct codes

woven together by a Python3 framework called NEXUS.

Theoretical methods for fission

We could try to build our model from the ground up using quantum mechanics - this is hard

Energy-density functional theory (DFT) calculations are built on this approach

Can give key physical insight into system of interest

Drawbacks stem from uncertainty in choice of functionals and high computational costs

Or...

View the nucleus as a liquid drop composed of macroscopic and microscopic terms - less hard

Macroscopic-microscopic methods are based on this approach

Fast and scalable; good for performing global calculations

Drawbacks: these models are not self-consistent; dependent on fine-tuned parameters

A basic picture of fission

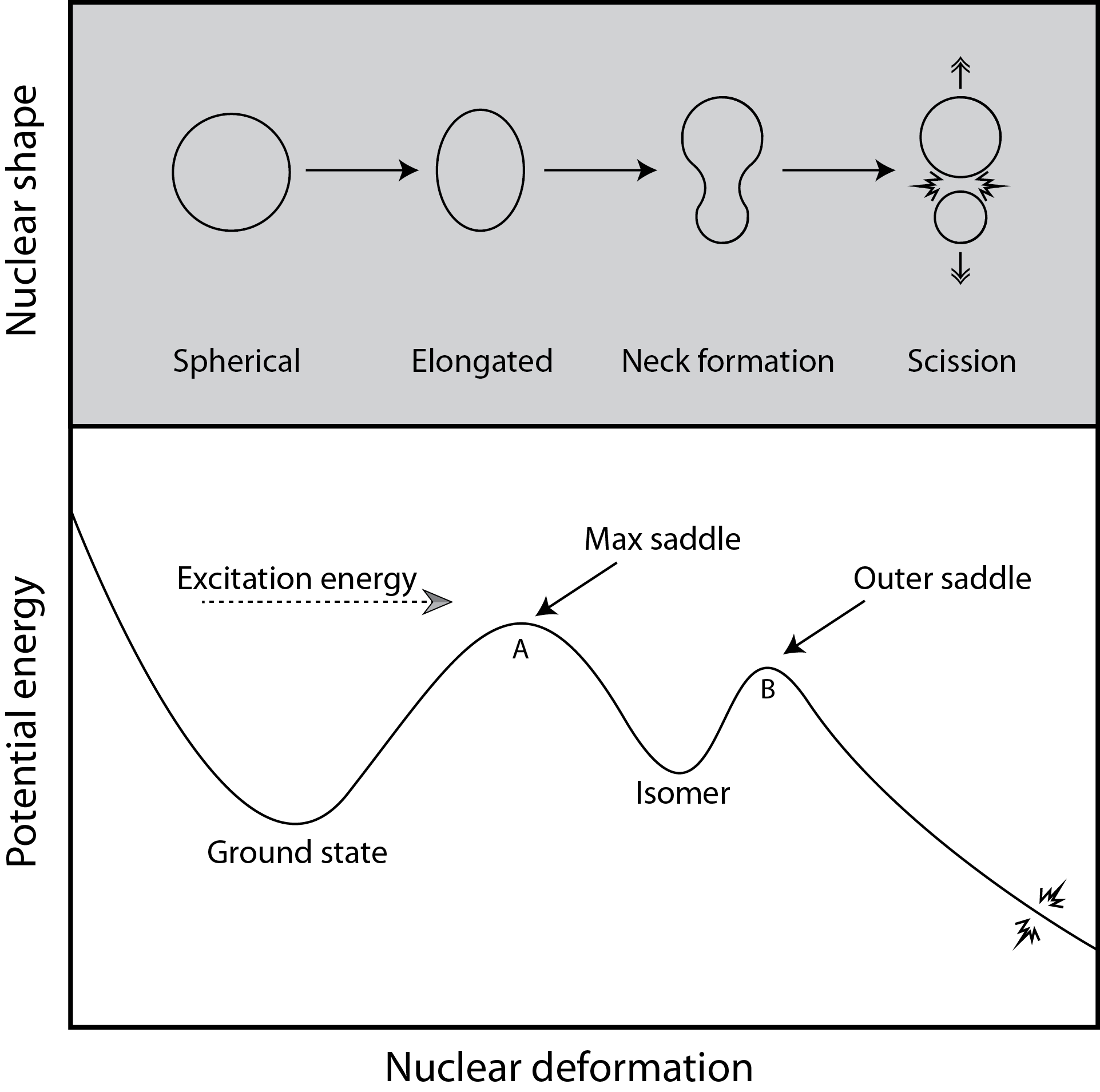
Follow progression of the nucleus from compact to highly elongated shapes

Finite-Range Liquid-Drop Model

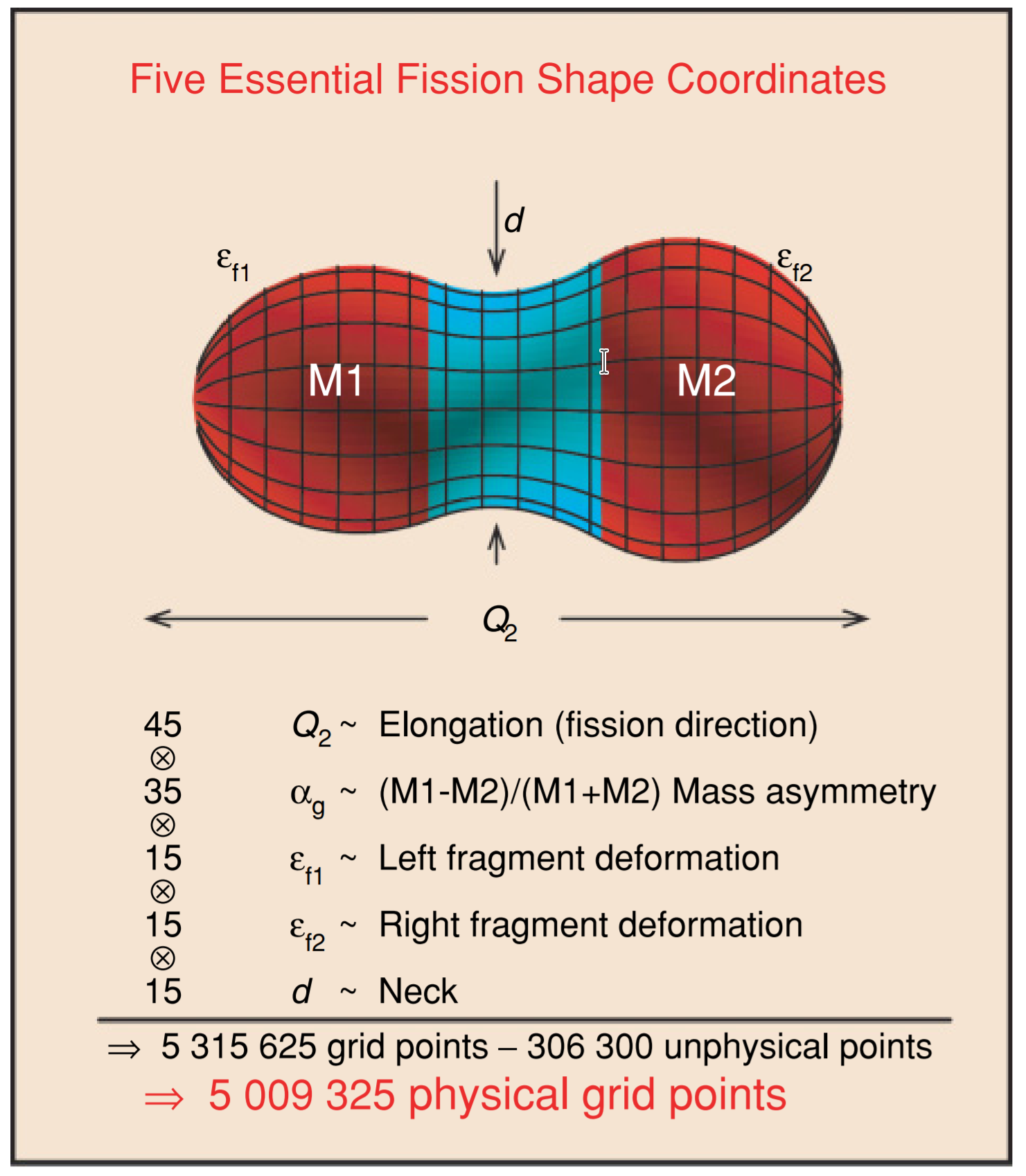
Many possible shape degrees of freedom - but we have to isolate the most important

Calculation of nuclear potential energy surfaces

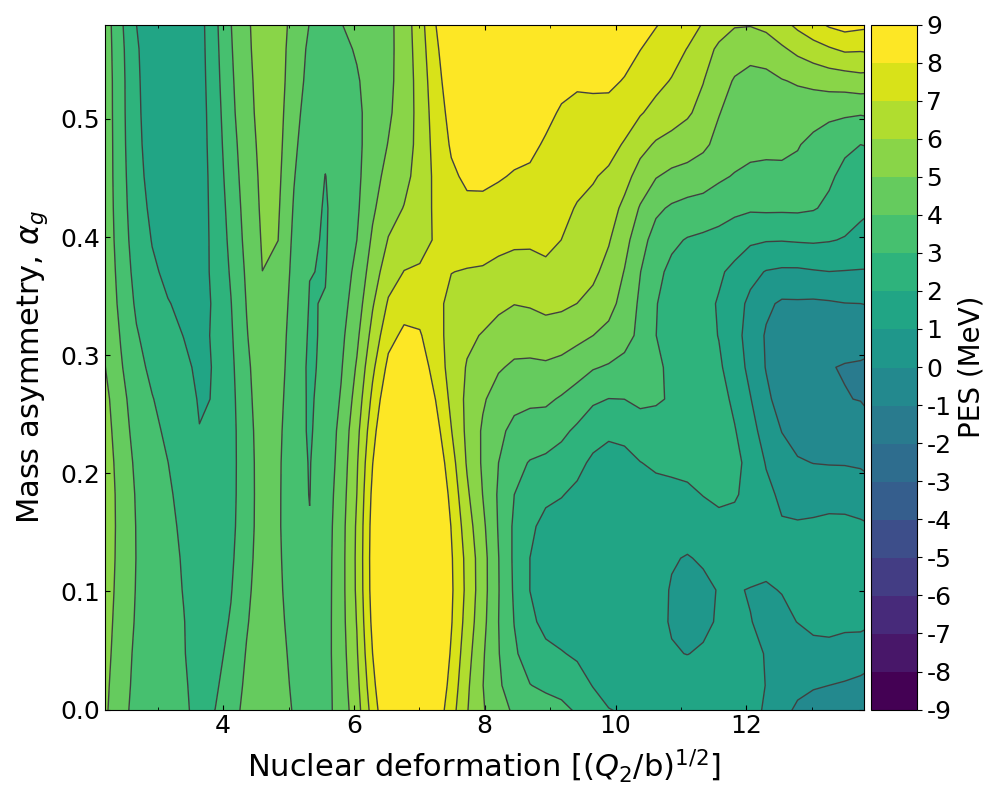
Projected potential energy surface from 5 canonical shape parameters of FRLDM

Path to sission is dependent on the trajectory through this complex surface

Nuclear potential energy surface of 236-U

Calculation of fission yields

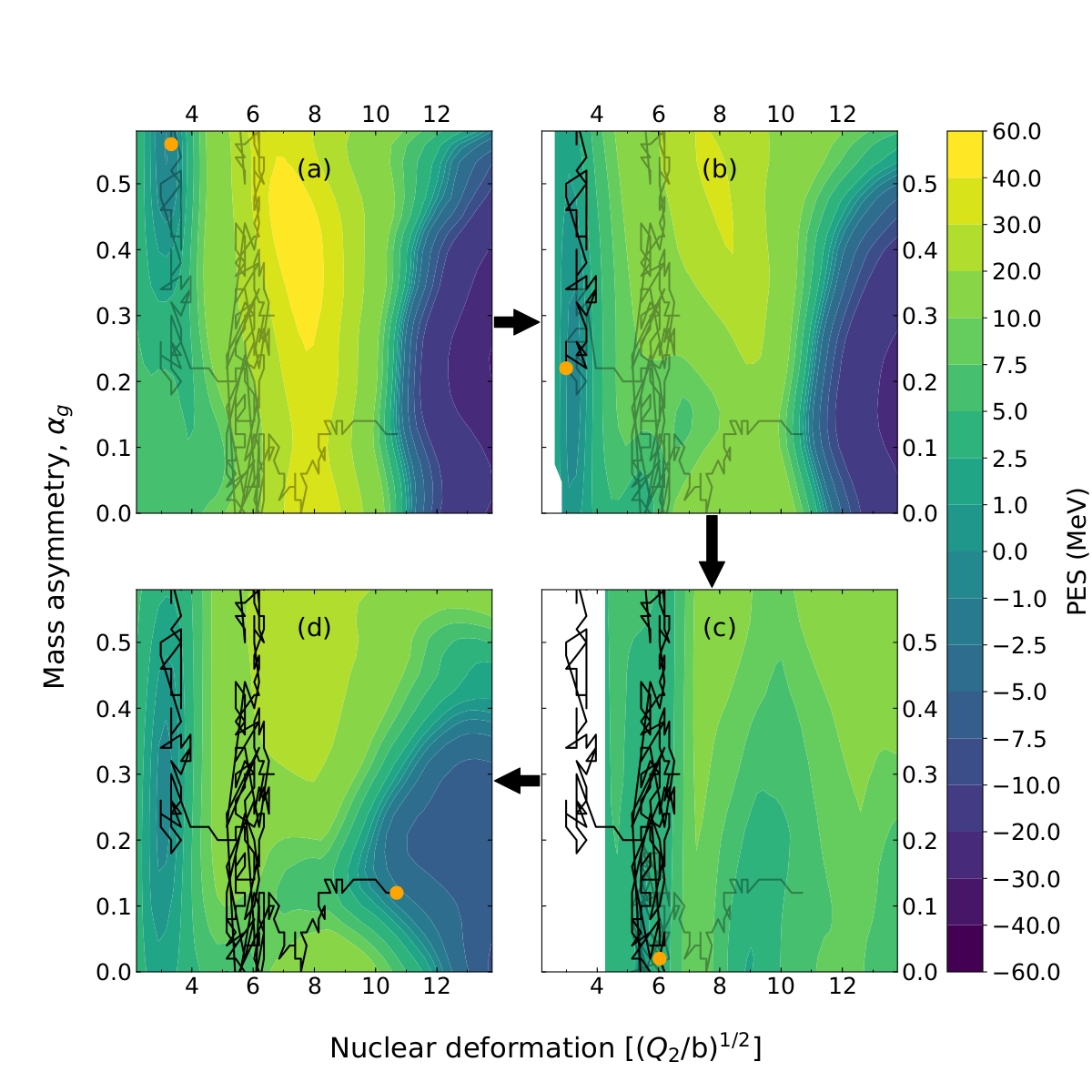
Change in nuclear shape acts as a driving force for bulk rearrangement of material

Amounts to random walk across potential energy surface

Theoretical primary yield compared to data

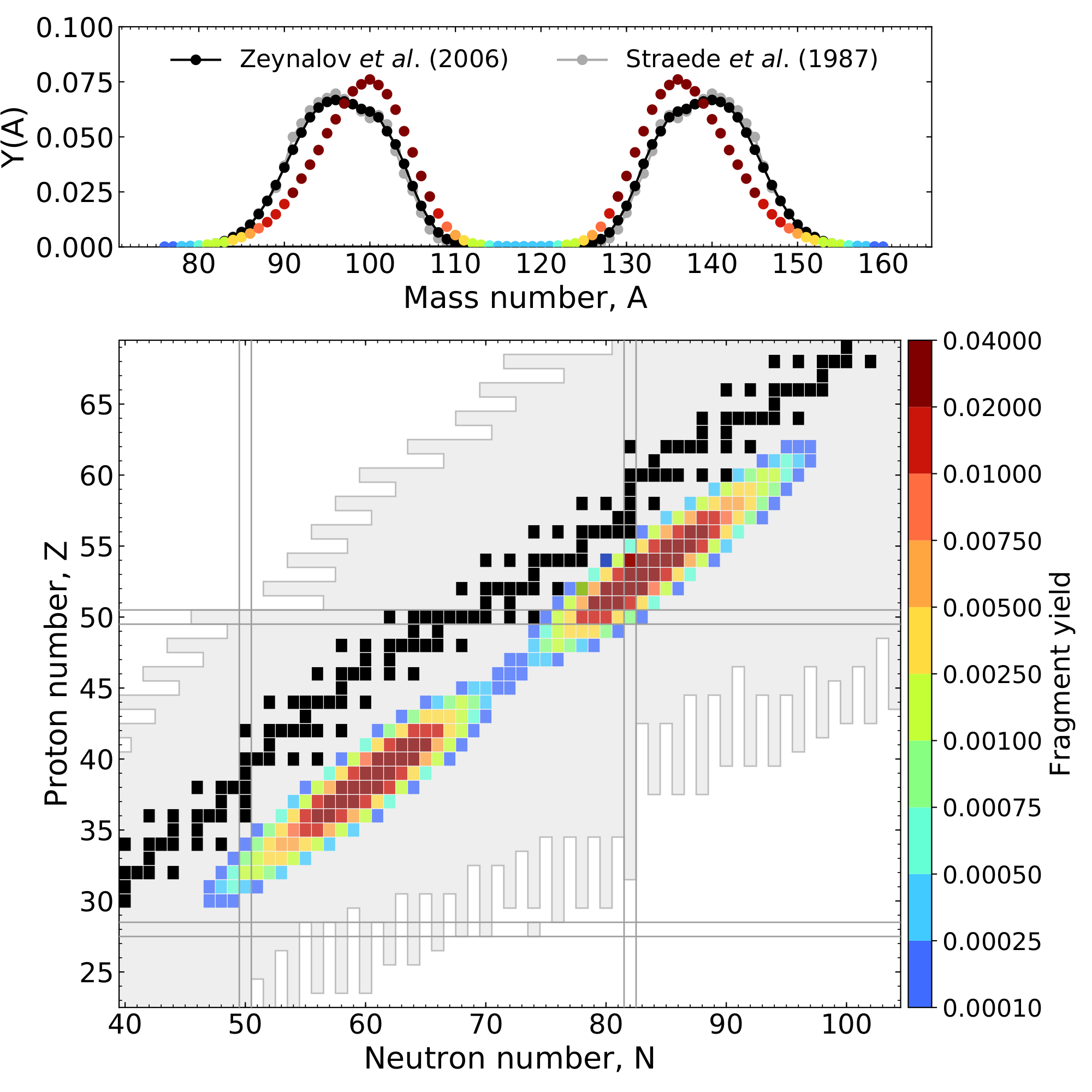
Ensemble of fission events leads to the cumulation of the yield curve ($^{235}$U + n$_{\rm{therm}}$)

Relies on geometric splitting argument for the scission configuration

Charge yield with odd-even staggering

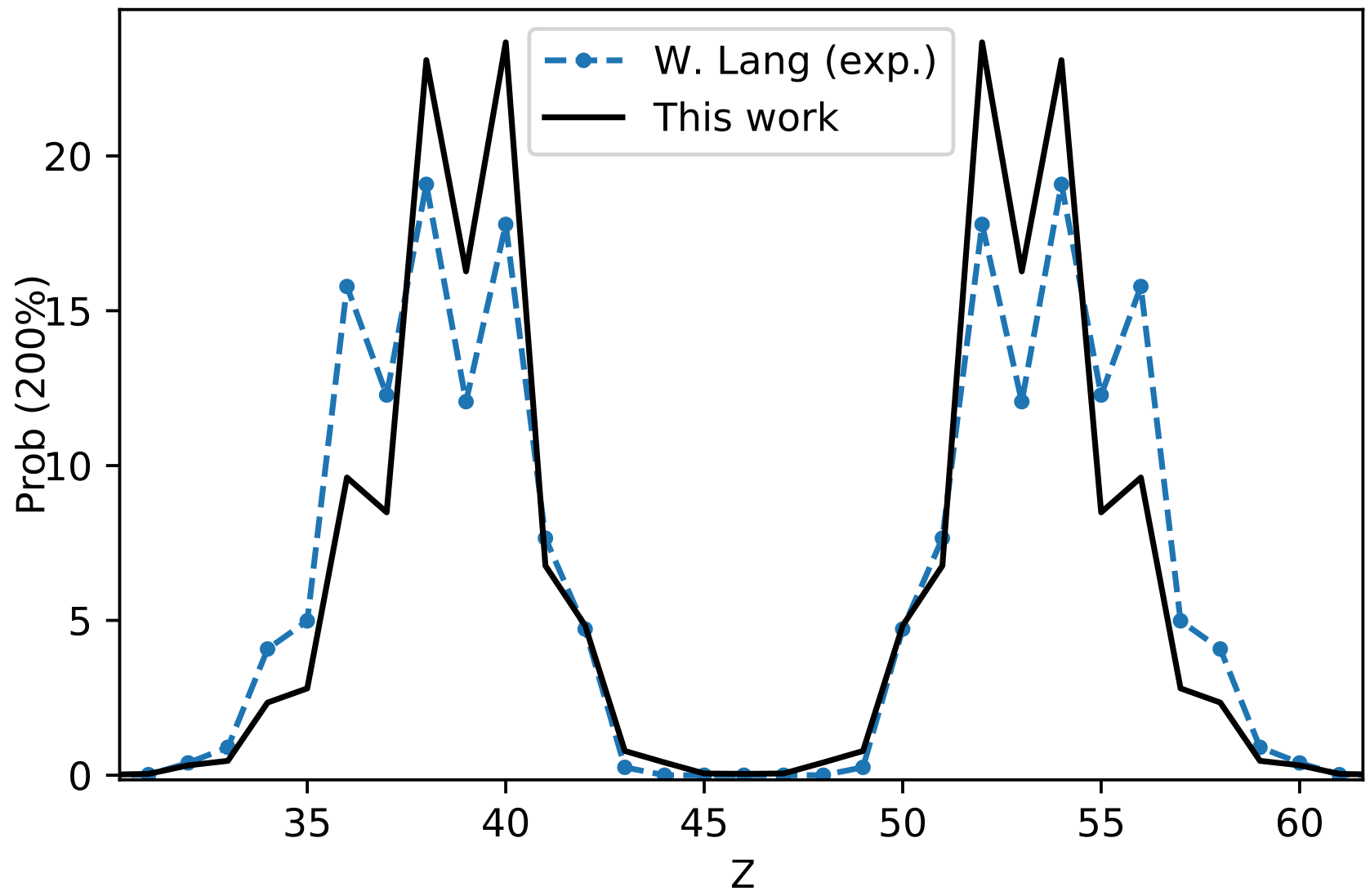
We have further enhanced these calculations; moving beyond the geometric picture

First theoretical prediction of odd-even staggering using a particle number projection technique for $^{235}$U + n$_{\rm{therm}}$

Even more improvement when larger quantum basis is used (recall Marc Verriere's talk)

BeOH: statistical de-excitation

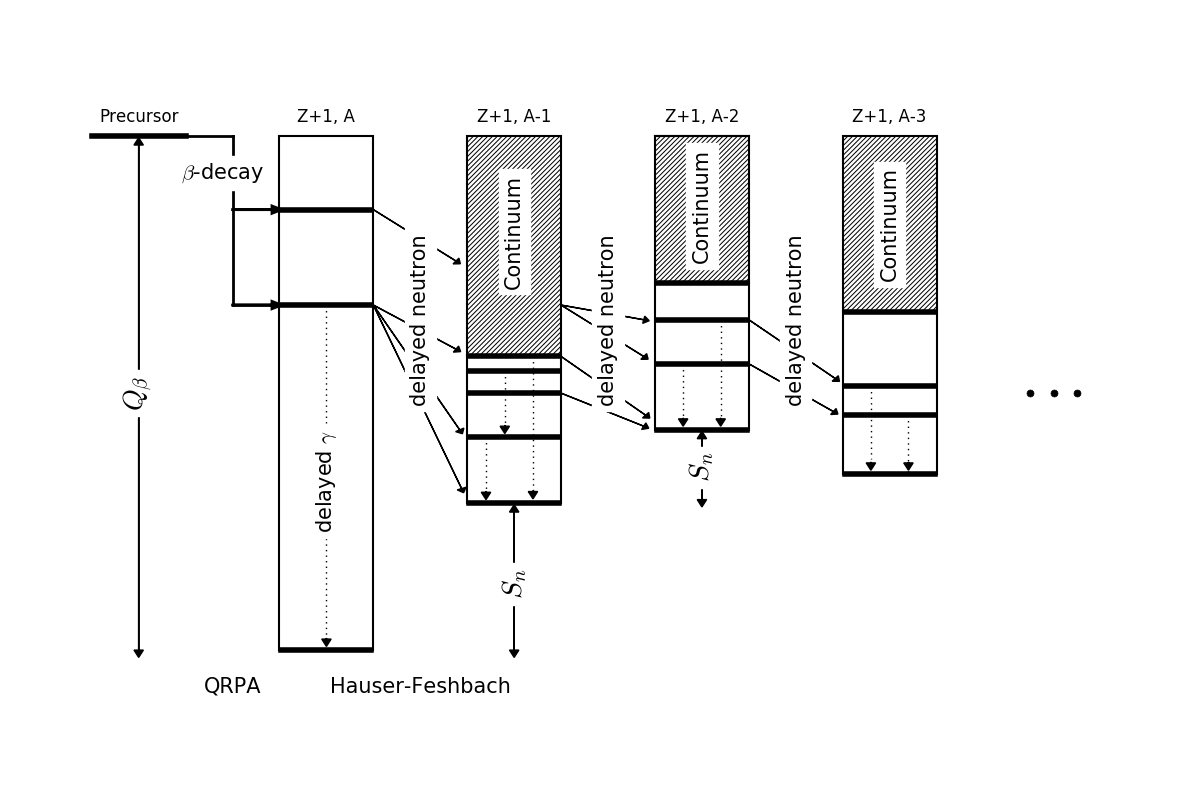
Assume Bohr indepdence hypothesis of compound nucleus formation

Can study n, $\gamma$ and fission competition with $\beta$-decay

Used to study $\beta$-delayed neutron emission and multi-chance $\beta$-delayed fission (new decay mode)

Recently has been applied to statistical de-excitation of nascent fission fragments

Calculation of independent yield

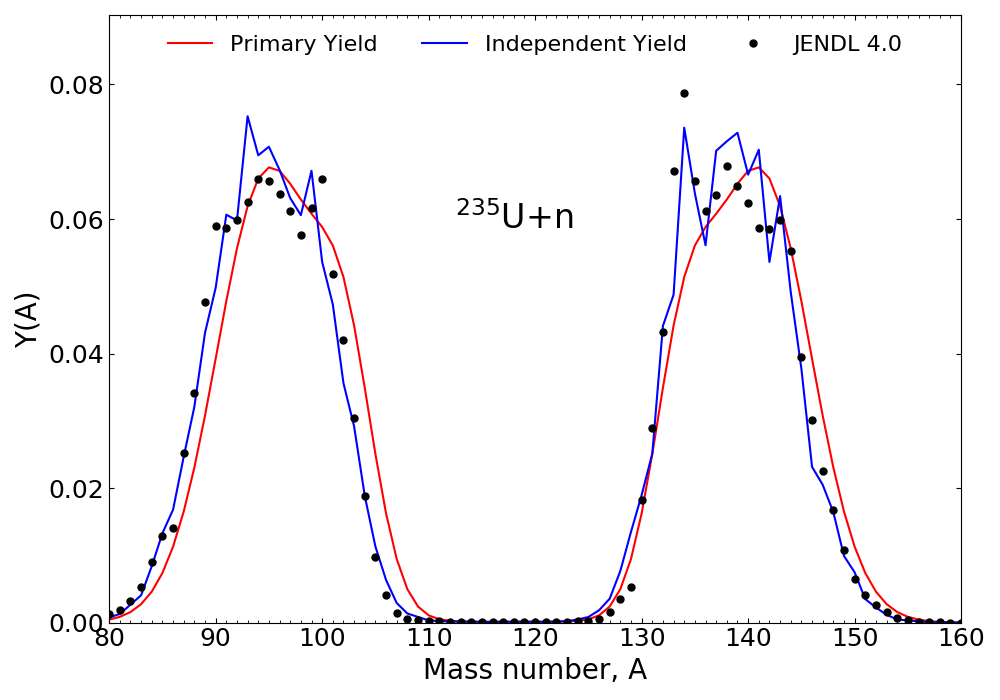
Fit data: Hambsch for $^{235}$U + n thermal fission

Primary yield (PY): using 5D Gaussian fitting procedure; charge systematics from Wahl

Independent yield (IY): after prompt neutron and $\gamma$-ray emission using BeOH / HF$^3$D

Average prompt neutrons

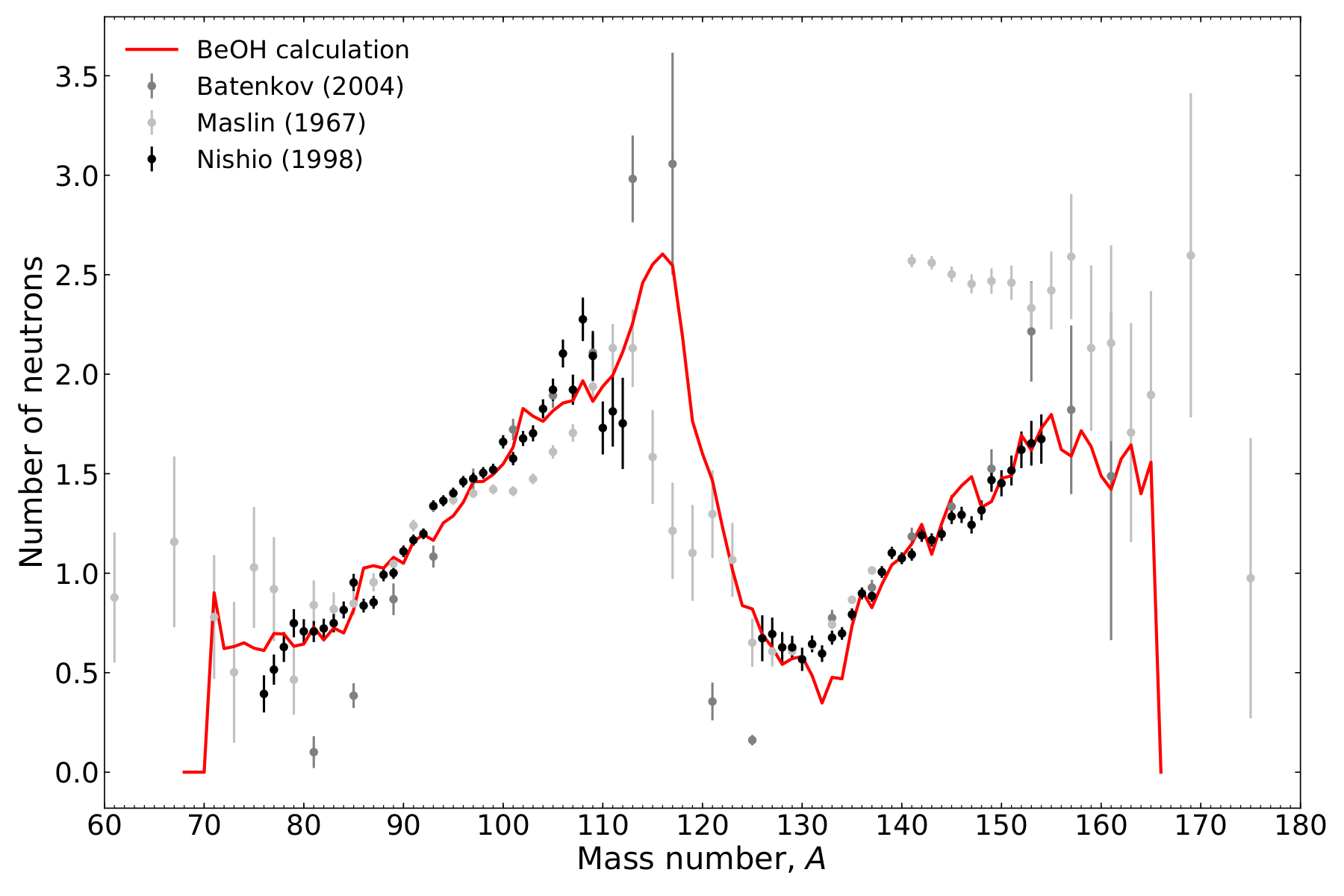
Average prompt neutrons emitted as a function of fragment mass number

Critical inputs: yield; total kinetic energy as a function of mass number and excitation energy sharing

Increasing confidence of using these models for our evaluation efforts

Auxiliary outputs

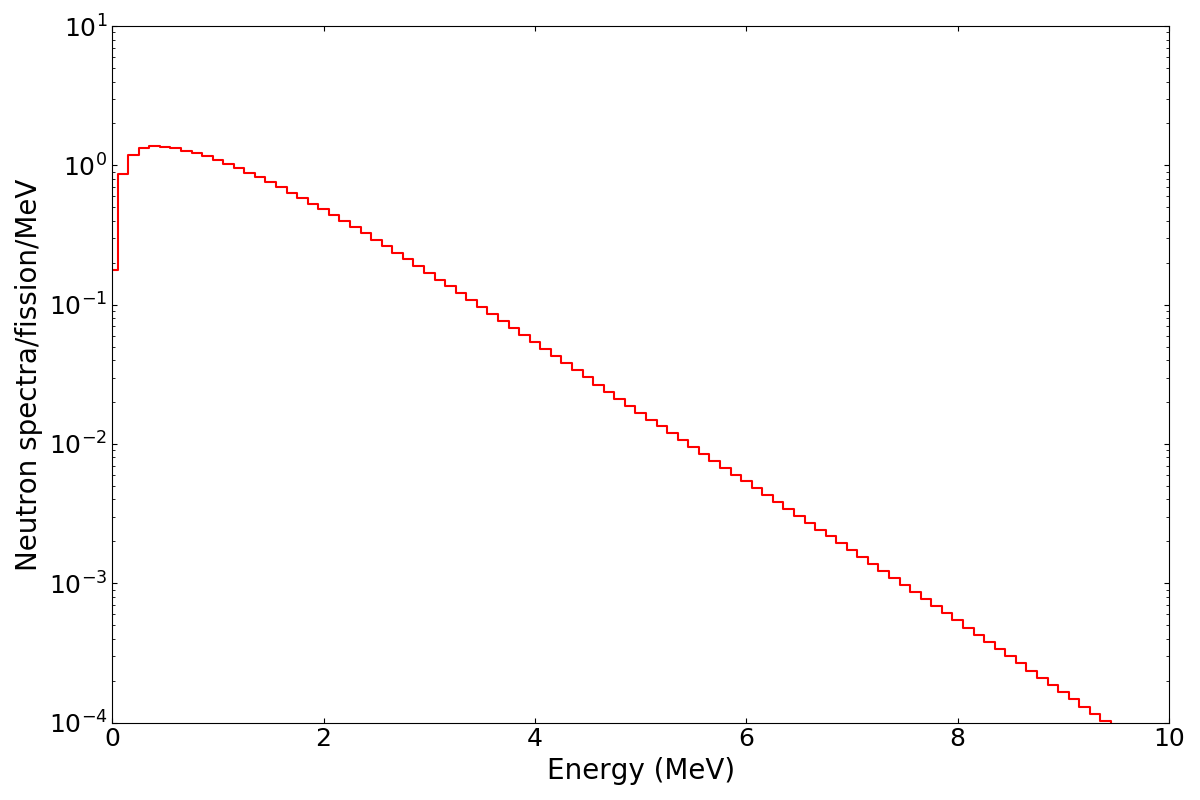
Consistently calculated with the independent yield

Prompt neutron spectrum; prompt gamma spectrum

Particle multiplicities: P($\nu$), P($N_\gamma$)

Uncertainties & Correlations

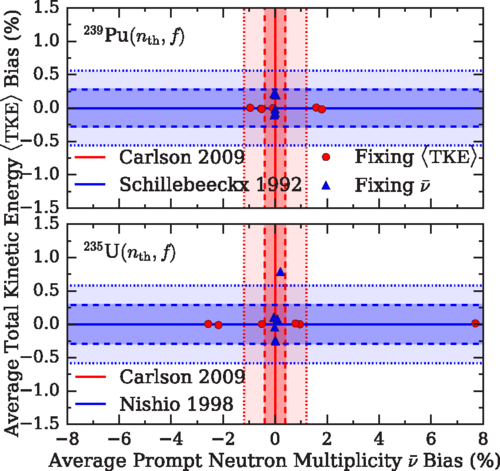
Statistical & systematic uncertainties from experiment

Propagation of parameter uncertainties

Model defects

Summary

Current fission evaluations have not been updated in years

and are further lacking for modern applications

An effort to produce an improved fission yield evaluation is underway

We have made major advances in:

Nuclear potential energy surfaces ▴ fission yield calculations ▴ statistical de-excitation

We seek to:

• incorporate new data from recent experiments
• provide consistency between yields, n's & $\gamma$'s, and decay data
• include more continuous energy dependent information
• include time-dependent information (e.g. isomeric ratios)

We are planning to include this new fission yield evaluation in the next ENDF release