Modeling masses with an artificial neural network


LA-UR-22-31213
Matthew Mumpower
Fall DNP
Friday Oct. 28$^{th}$ 2022

Theoretical Division

Los Alamos National Laboratory Caveat
The submitted materials have been authored by an employee or employees of Triad National Security, LLC (Triad) under contract with the U.S. Department of Energy/National Nuclear Security Administration (DOE/NNSA).
Accordingly, the U.S. Government retains an irrevocable, nonexclusive, royaltyfree license to publish, translate, reproduce, use, or dispose of the published form of the work and to authorize others to do the same for U.S. Government purposes.
Mixture Density Network
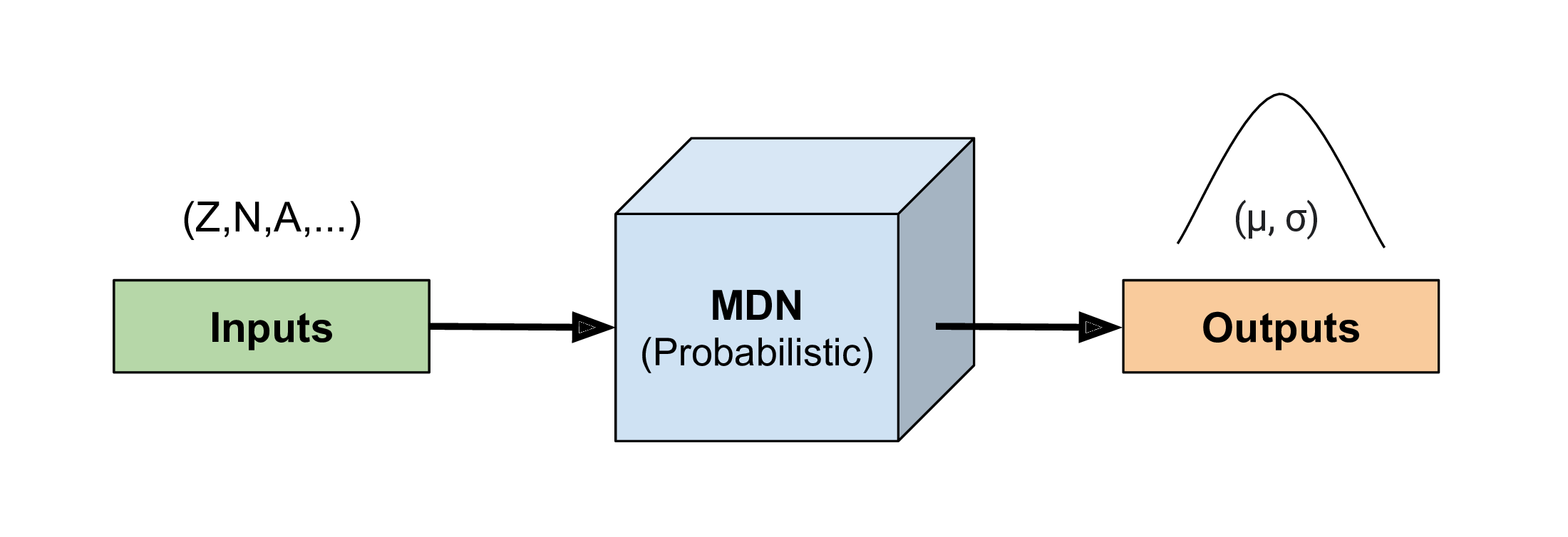
We take a Bayesian approach: our network inputs are sampled based on nuclear data uncertainties
Our network outputs are therefore statistical
We can represent outputs by a collection of Gaussians (for masses we only need 1)
Our network also provides a well-quanitfied estimate of uncertainty (fully propagated through the model)
Network topology: fully connected $\sim$4-8 layers; 8 nodes; regularization via weight-decay
Last layer converts output to Gaussian ad-mixture
An MDN for atomic masses
Writing down the many-body quantum mechanical Hamlitonian is hard; want to find ground state
Set: $f(\vec{\boldsymbol{x}}) = \vec{\boldsymbol{y}}$
$f$ will be a neural network (a model that can change)
$\vec{\boldsymbol{y}_{obs}}$ are the observations (e.g. Atomic Mass Evaluation) we want to match $\vec{\boldsymbol{y}}$ with
But what about $\vec{\boldsymbol{x}}$?
Why not a physically motivated feature space!?
proton number ($Z$), neutron number, ($N$), nucleon number ($A$), etc.
This is a contrasting approach than other avenues pursued in the literature
Past work relies on matching model residuals: $\vec{\boldsymbol{y}}$ = (model output) - data
Training on mass data
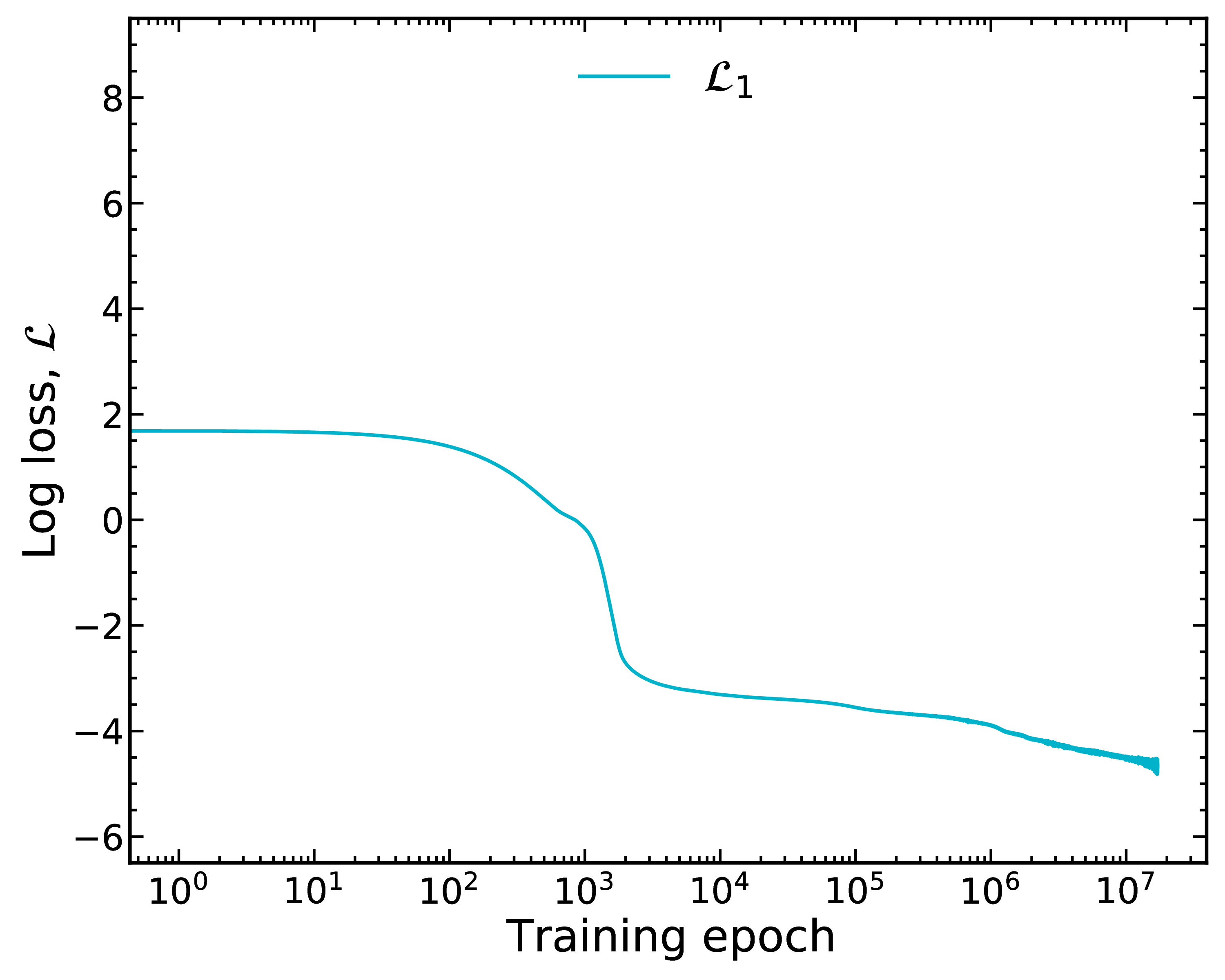
We train on mass data using a log-loss, $\mathcal{L}_1$
Training takes a considerably long time
Introduce physical constraint via loss function
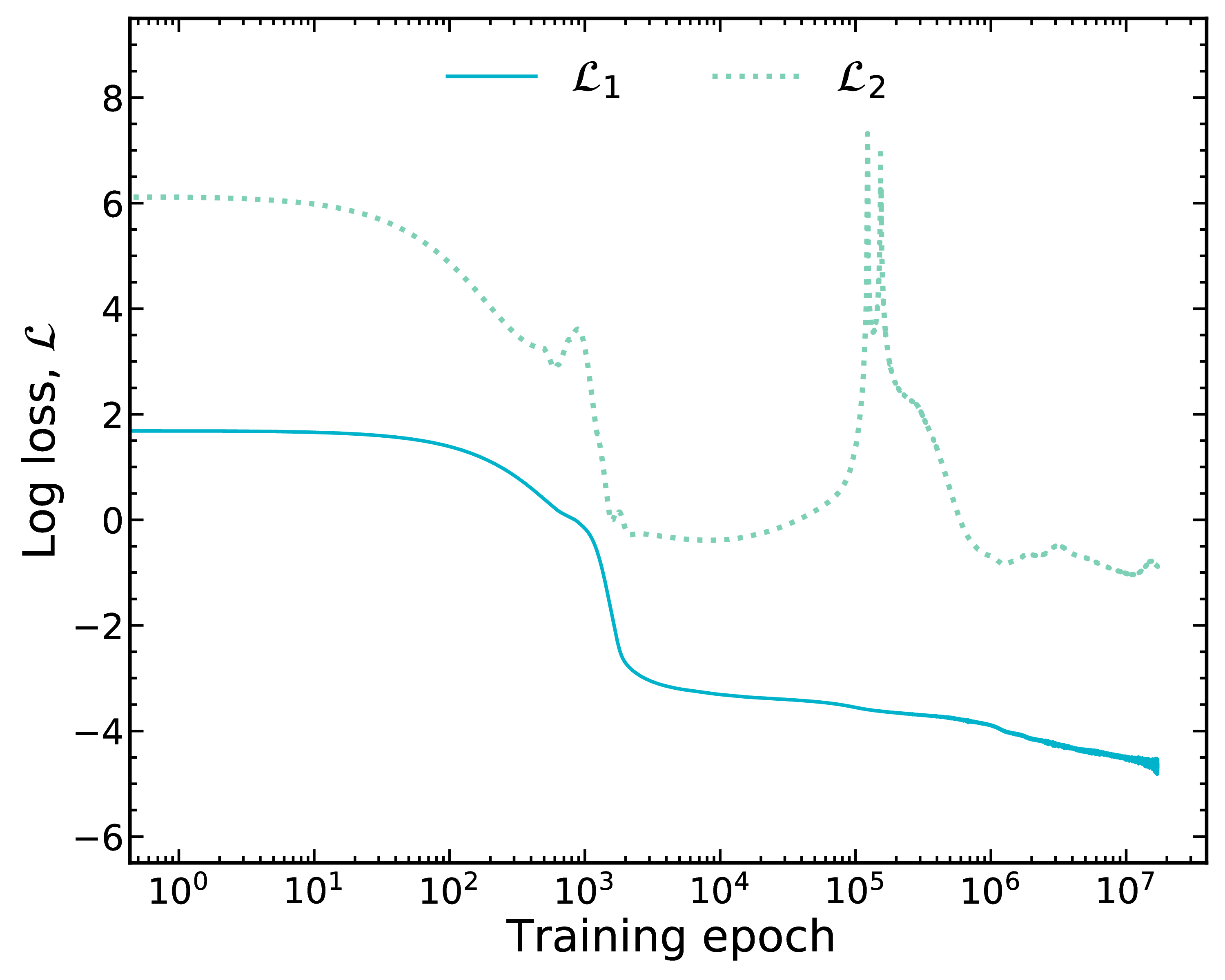
Now we optimize data, $\mathcal{L}_1$, and introduce a second (physical) constraint, $\mathcal{L}_2$
We have tried many physics-based losses, this particular one (Garvey-Kelson relations) performs well
Total loss: sum the two losses
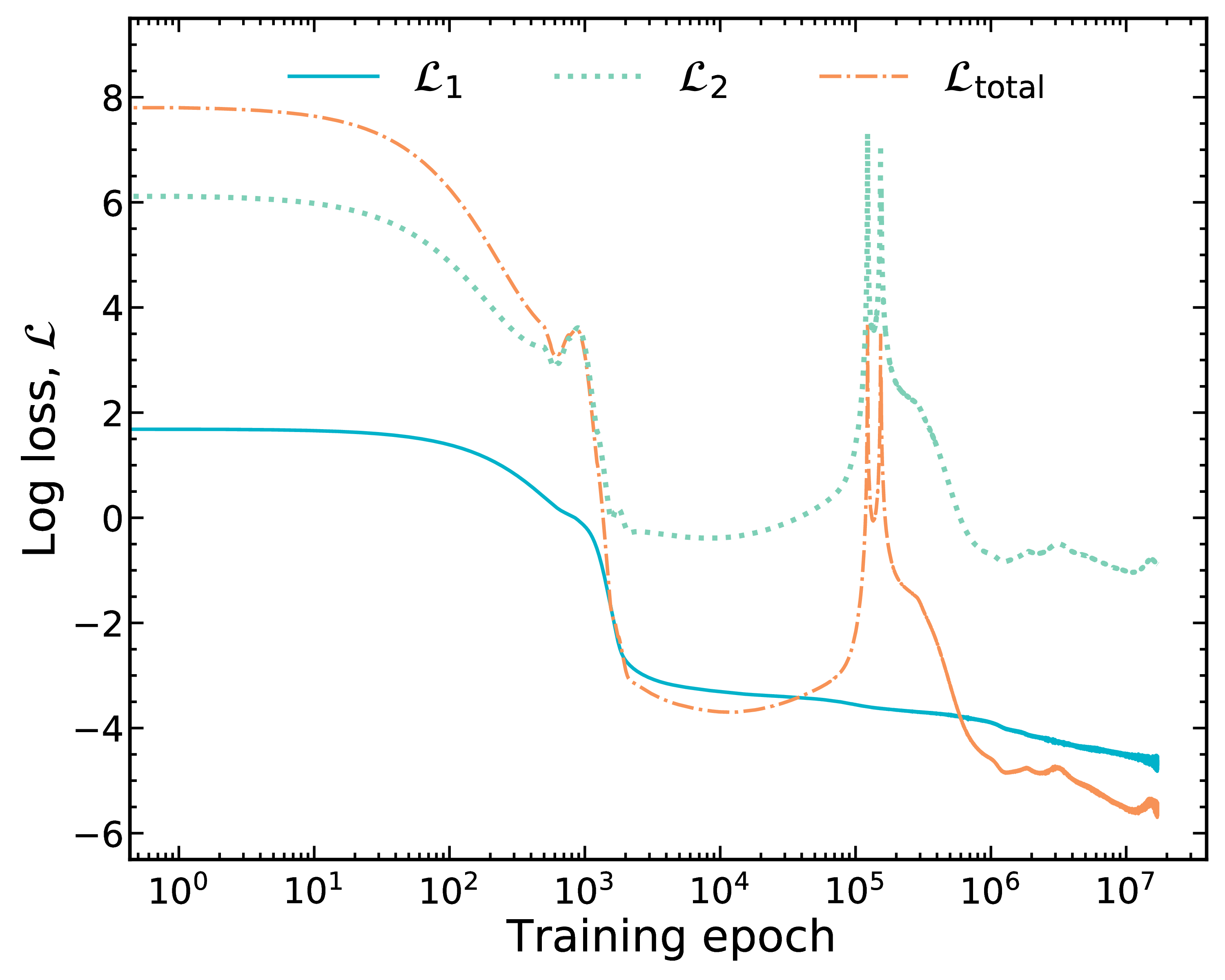
$\mathcal{L}_\textrm{total} = \mathcal{L}_1 + \lambda_\textrm{phys} \mathcal{L}_2$ ; $\lambda_\textrm{phys}=1$ in this case
Good match to data does not imply good physics (although by happenstance it is in the end in this case)!
Mass trends along Nd isotopic chain, $Z=60$
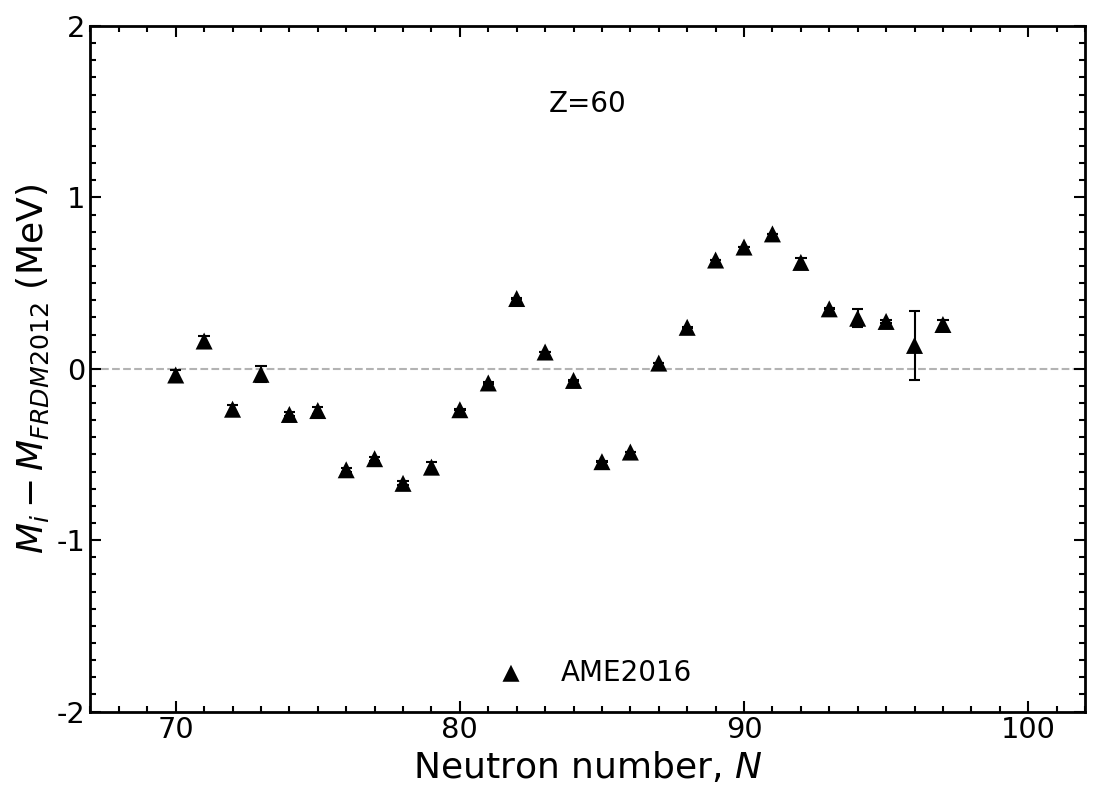
Results plotted relative to the Los Alamos FRDM model
Modern mass models draw a 'straight line' through data
Mass trends along Nd isotopic chain, $Z=60$
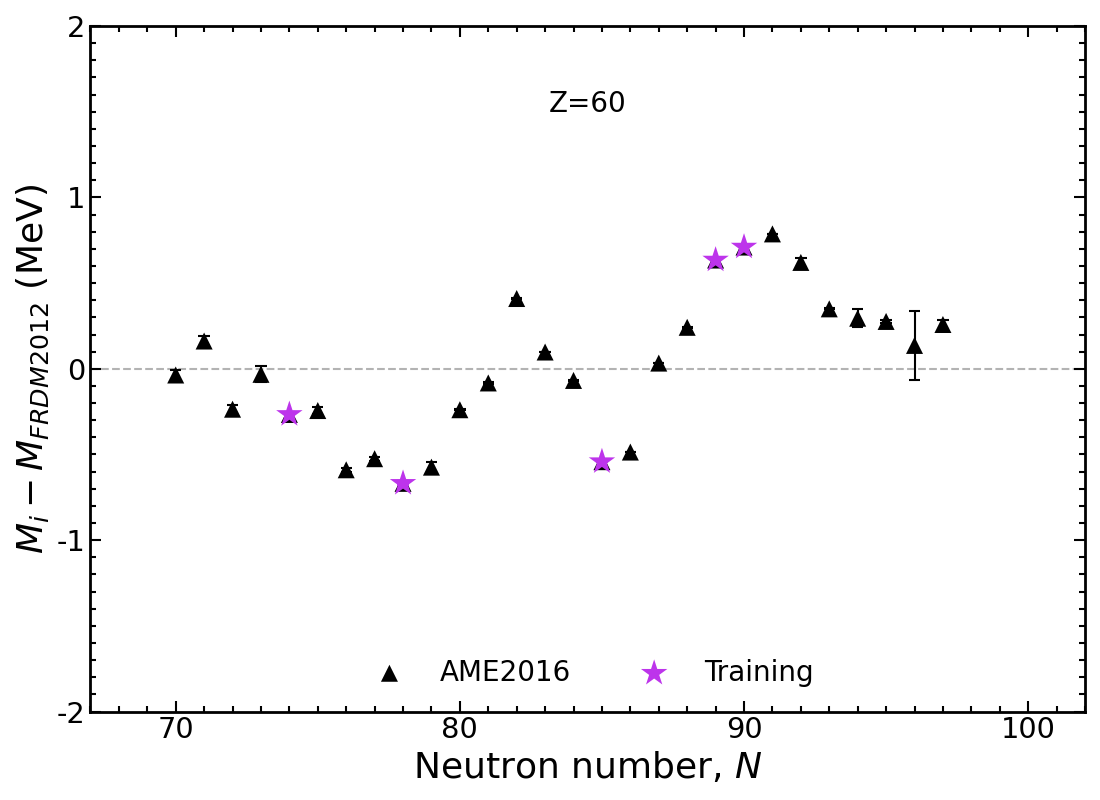
Train on only a few select nuclei (450 total, at random, across the chart of nuclides)
The rest of the chart (including AME points) are predictions
Mass trends along Nd isotopic chain, $Z=60$
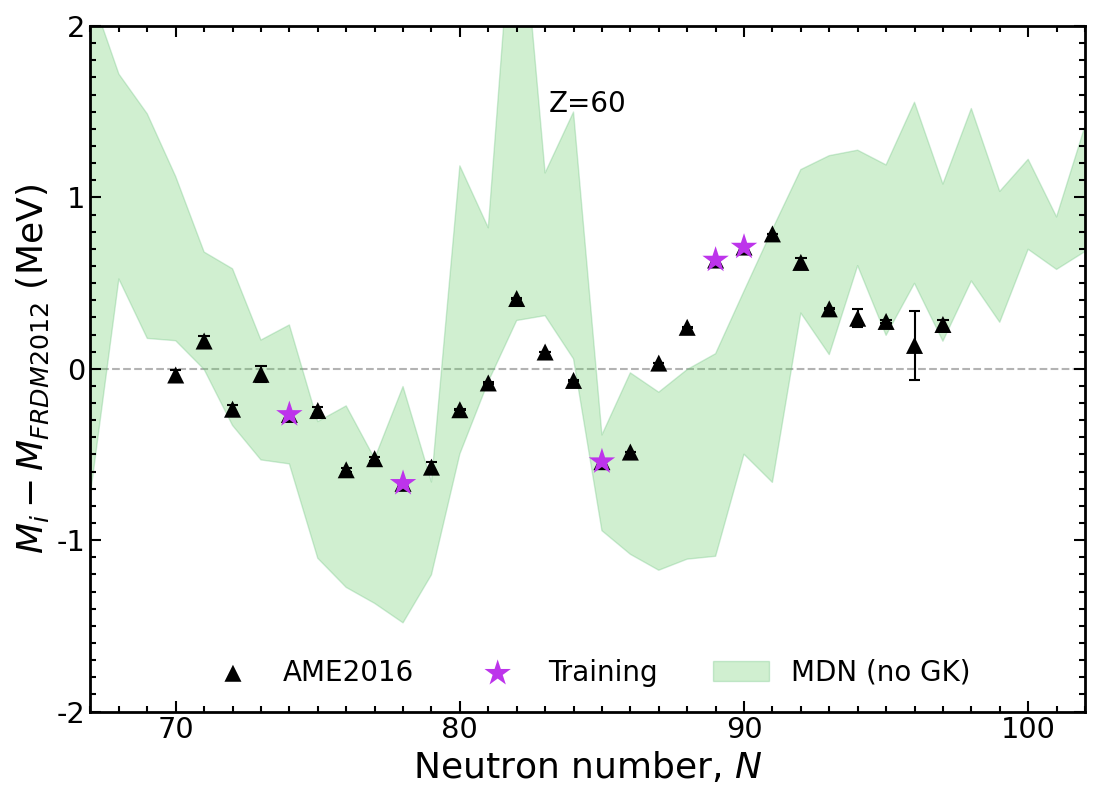
If we use no physics information in training the spread in predictions is large
Trends can be obtained, but models lack accuracy
Results of new model Nd, $Z=60$
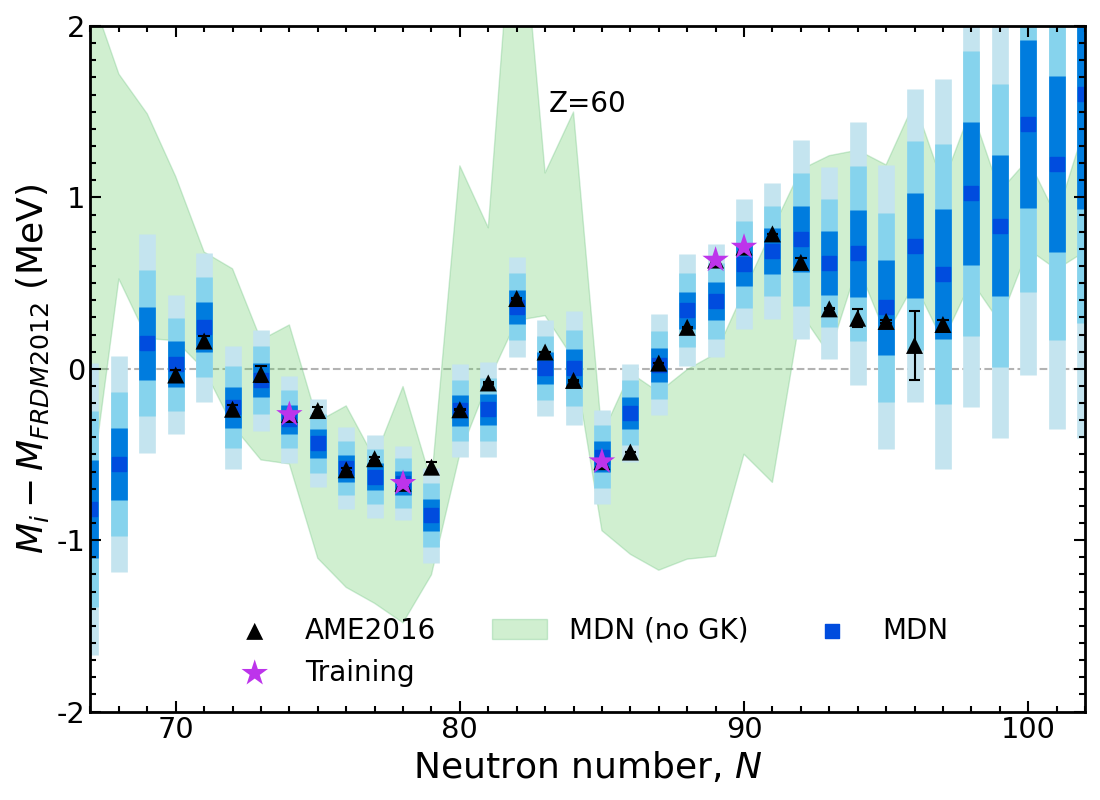
Including physics constraint provides superior model predictions
Probabilistic network → well-defined uncertainties predicted for every nucleus ( ◼ 1$\sigma$, ◼ 2$\sigma$ ◼ 3$\sigma$)
Results of new model Nd, $Z=60$
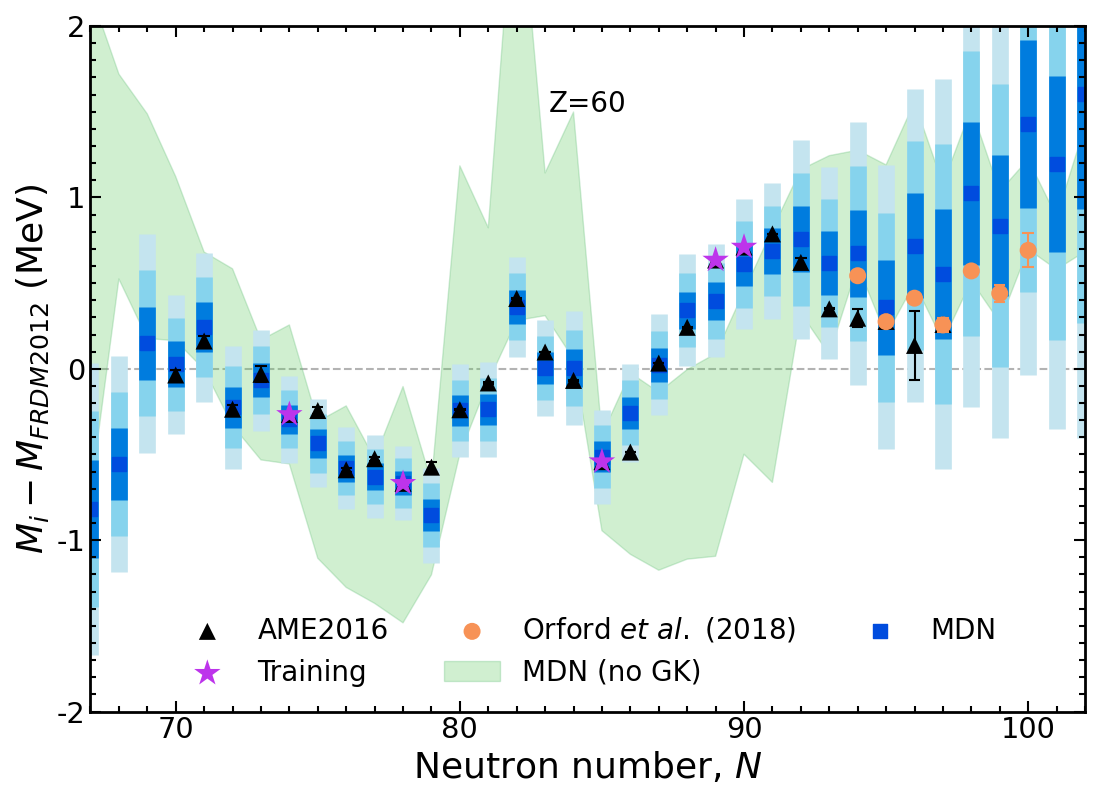
New data (unknown to the model) are in agreement with the MDN model predictions
Model is now trained on only 20% of the AME and predicting 80%!
The training set is random; different datasets perform differently
Results of new model Nd, $Z=60$
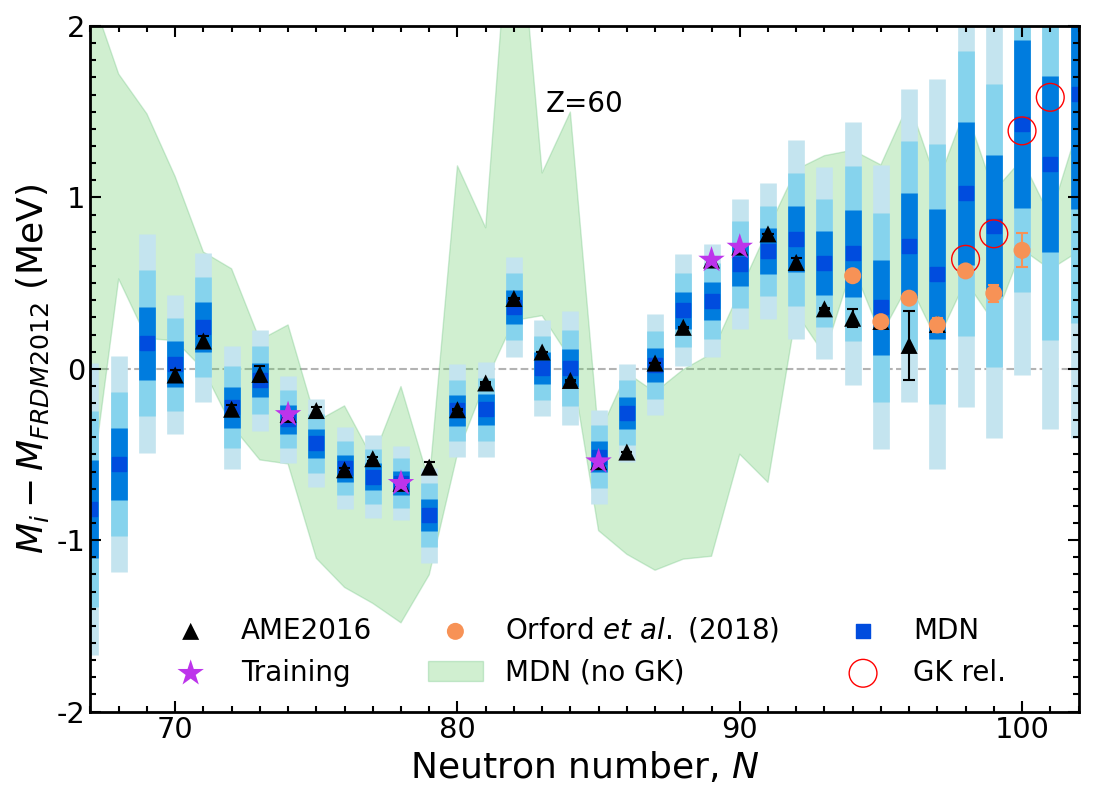
Using GK relations alone (red) quickly diverges due to accumulated errors from repeated iteration
Importantly, our model training enforces a single iteration of GK across the chart of nuclides!
Results of new model In, $Z=49$
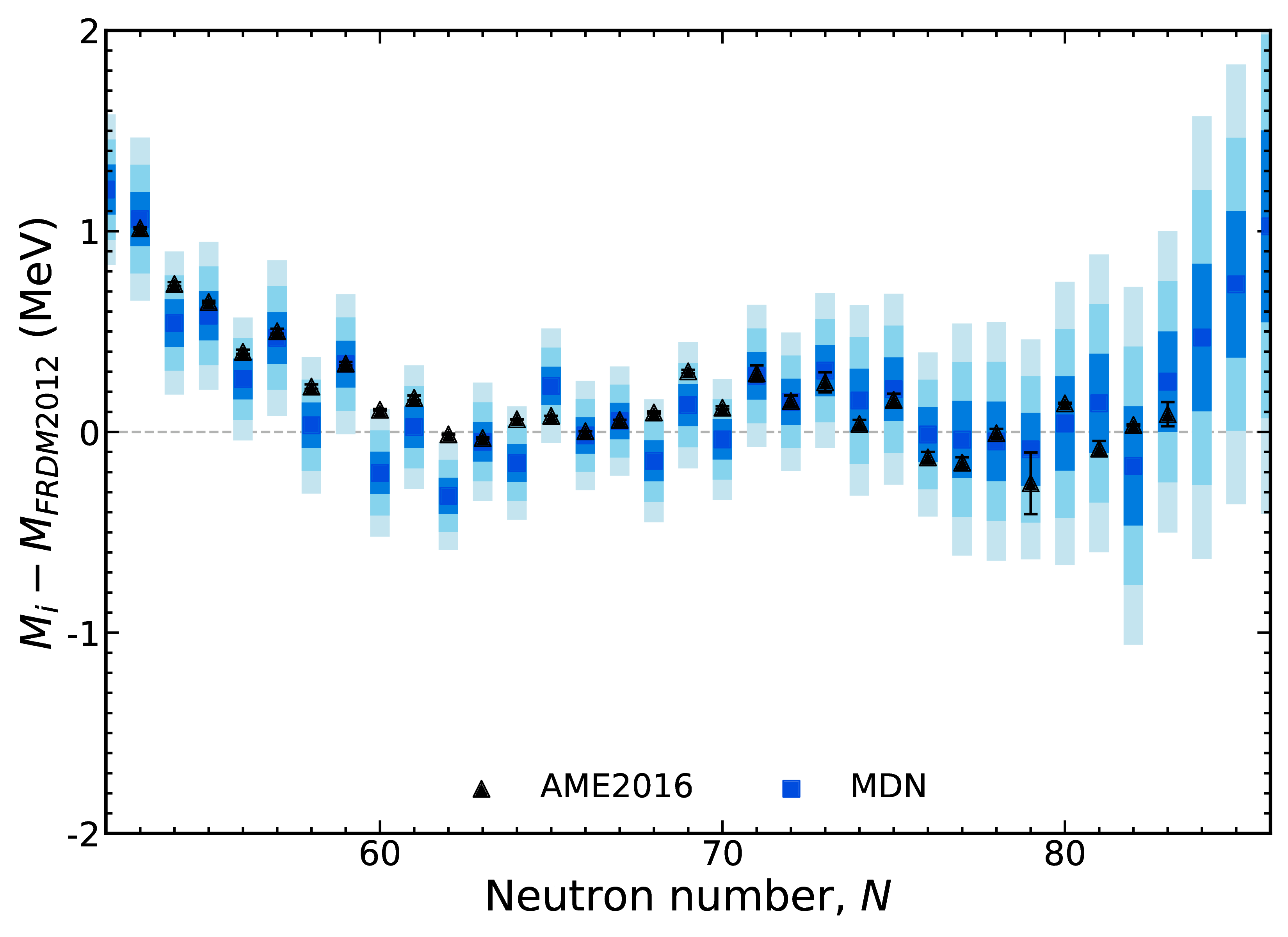
Our results are not limited to any mass region - all of them are described equally well ($Z \geq 20$)
Results are better than any existing mass model; uncertainties inherently increase with extrapolation
We can predict new measurements and capture trends (important for astrophysics)
How can we interpret these results?
One method is to calculate Shapley values (Shapely 1953 • Lundberg & Lee 2017)
Idea arises in Game Theory when a coalition of players (ML - features) optimize gains relative to costs
The players may contribute unequally, but the payoff is mutually beneficial
Applicable to many applications, ML in particular to understand feature importance
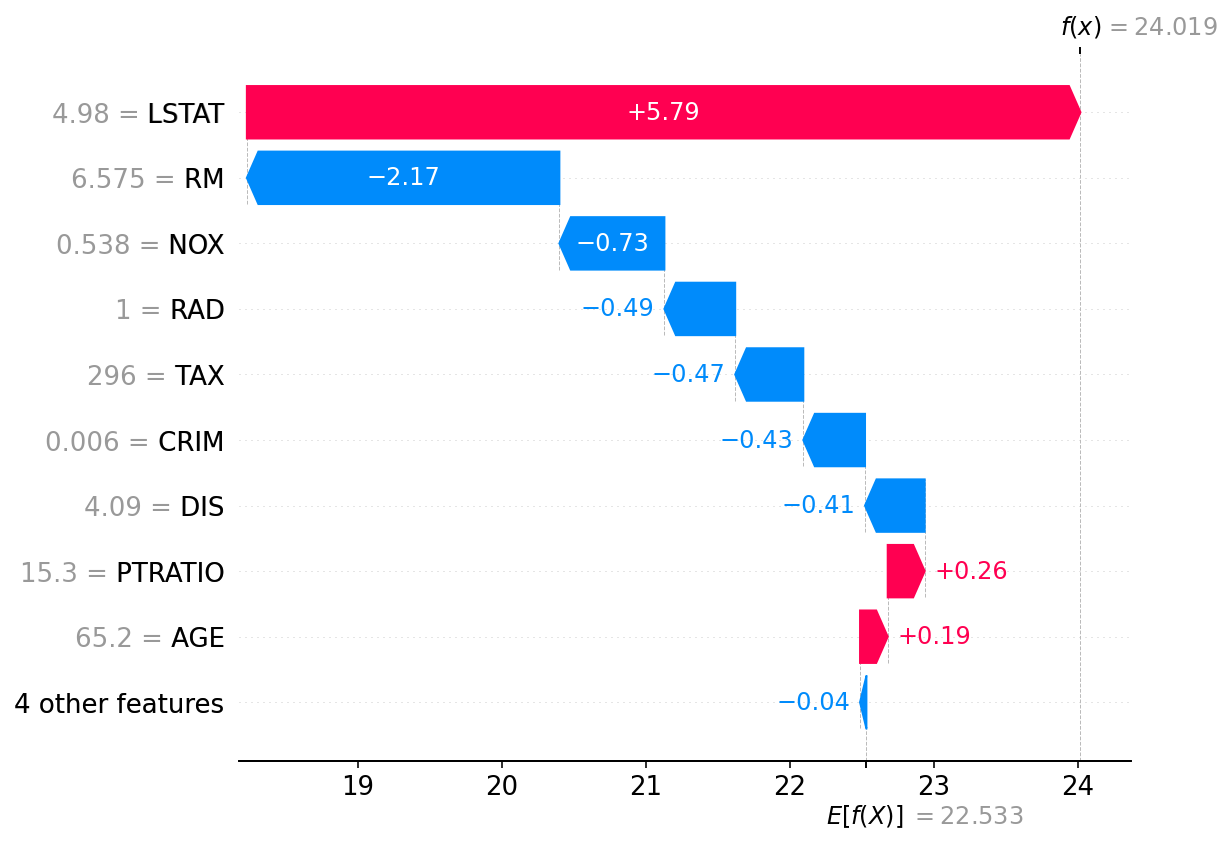
Ranking feature importance
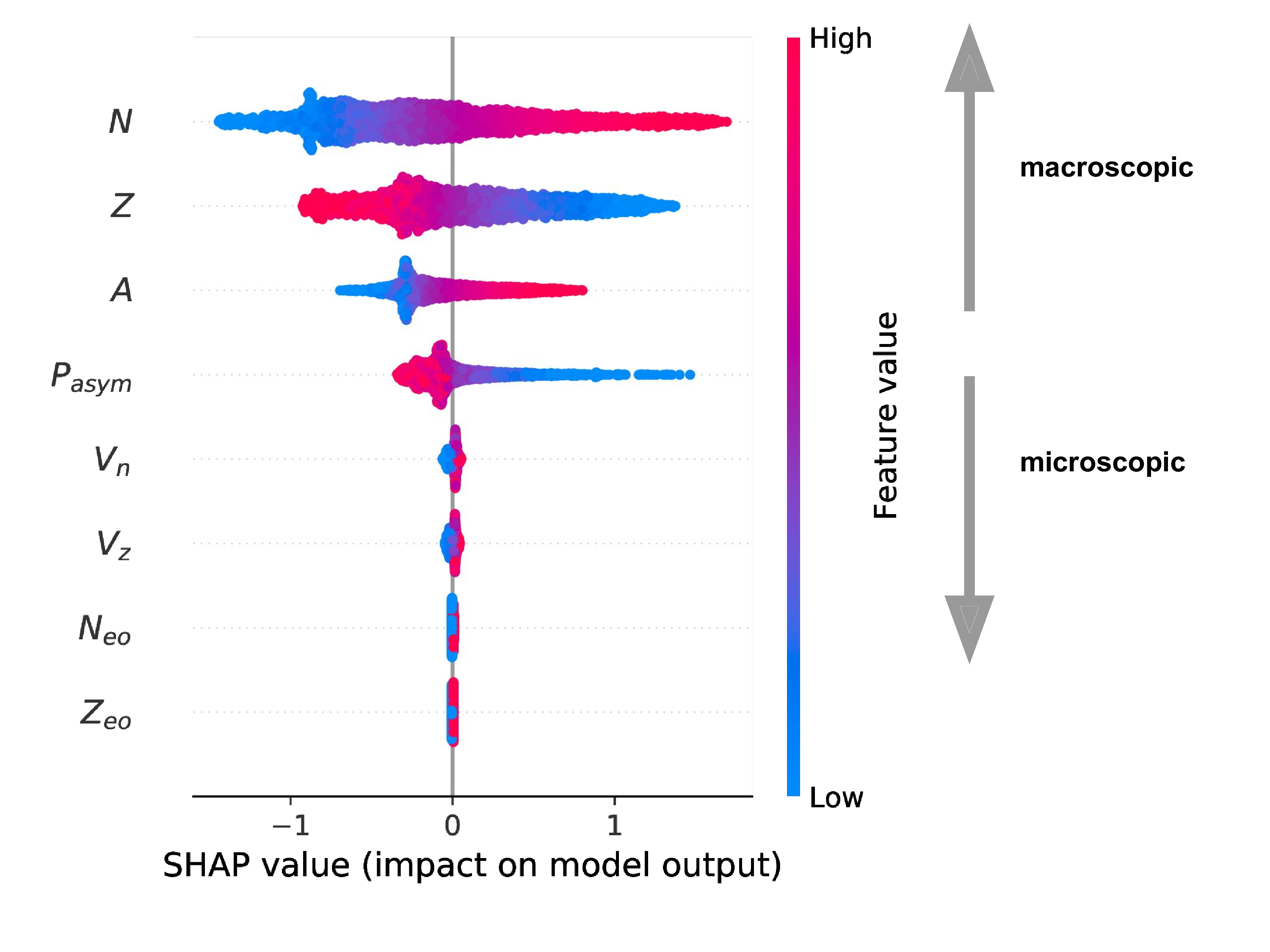
SHAP calculated for all of the AME (2020) [predictions!]
The model behaves like a theoretical mass model
Macroscopic variables most important followed by quantum corrections
What happens when there's new data? (generalization)
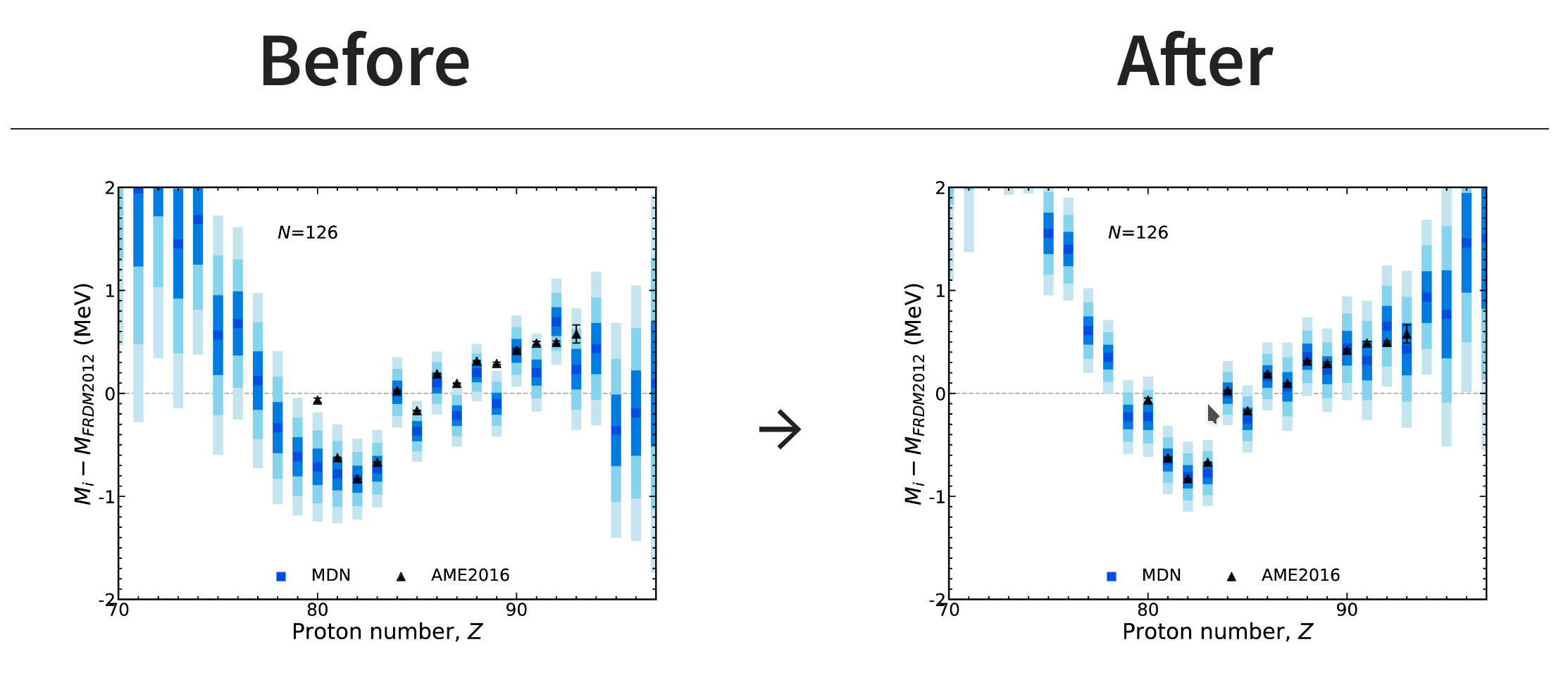
The network is able to incorporate this knowledge and updated predictions via Bayes' theorem
New information provided at closed shell $N=126$
Special thanks to
My collaborators
A. Lovell, A. Mohan, & T. Sprouse
▣ Postdoc
Summary
We have developed an interpretable neural network capable of predicting masses
Advances:
We can predict masses accurately and suss out trends in data
Our network is probabilistic, each prediction has an associated uncertainty
Our model can extrapolate and retains the physics
The quality of the training data is important (not shown)
We can classify the information content of existing and future measurements with this type of modeling
We are now ready to study the impact of this modeling in astrophysics!
Results / Data / Papers @ MatthewMumpower.com
