Simultaneous calculation of fission fragment charge and mass yields with the eFRLDM

LA-UR-21-30063
Matthew Mumpower
Fall DNP
Wednesday Oct. 13$^{th}$ 2021

Nuclear Data Team
Theoretical Division

Los Alamos National Laboratory Caveat
The submitted materials have been authored by an employee or employees of Triad National Security, LLC (Triad) under contract with the U.S. Department of Energy/National Nuclear Security Administration (DOE/NNSA).
Accordingly, the U.S. Government retains an irrevocable, nonexclusive, royaltyfree license to publish, translate, reproduce, use, or dispose of the published form of the work and to authorize others to do the same for U.S. Government purposes.
Why do we need fission yields?

Fission yields are needed for a variety of modern applications
Industrial applications: simulation of reactors, fuel cycles, waste management
Experiments: backgrounds, isotope production with radioactive ion beams (fragmentation)
Science applications: nucleosynthesis, light curve observations
Other Applications: national security, nonproliferation, nuclear forensics
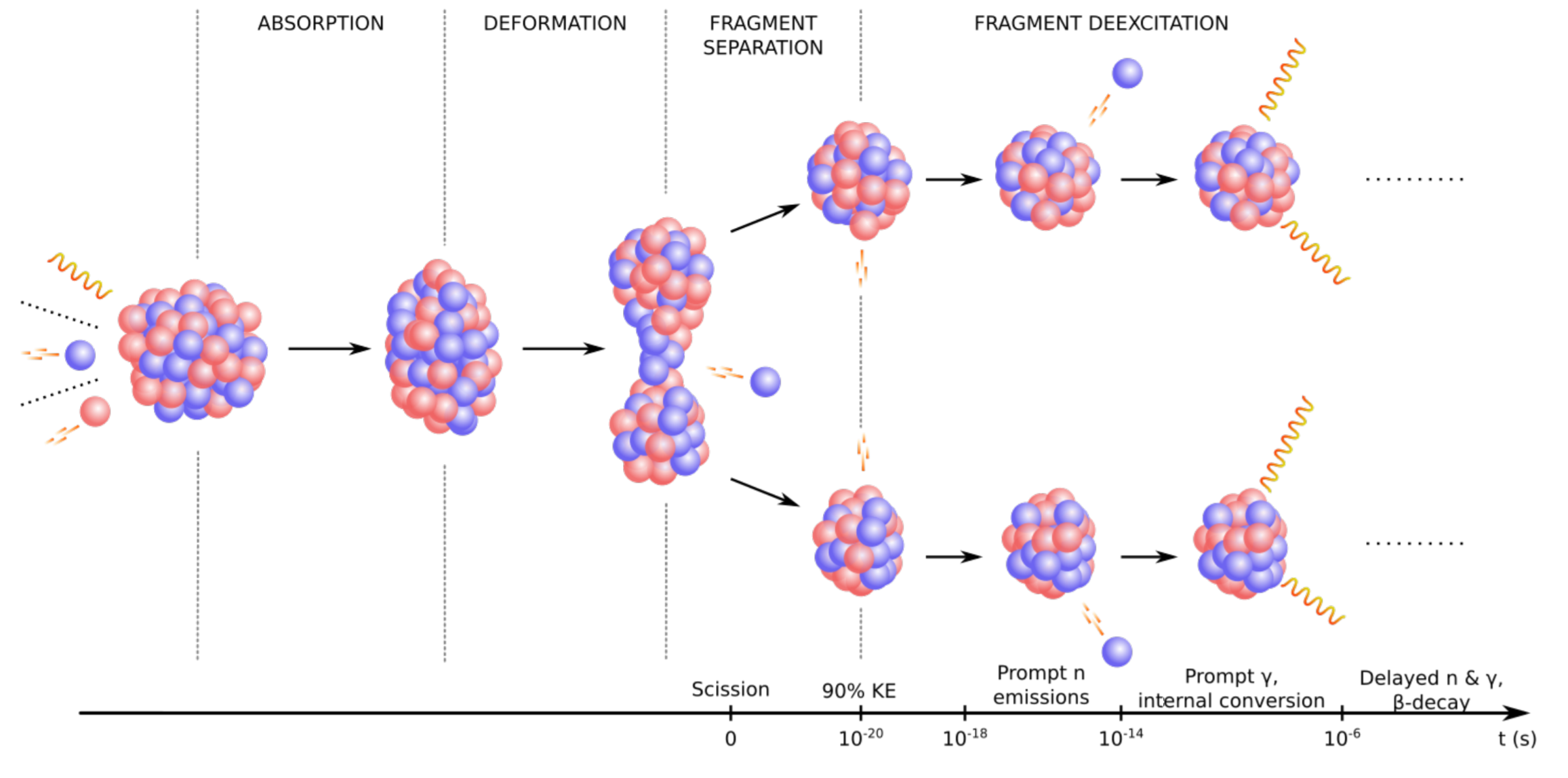
A basic picture of fission
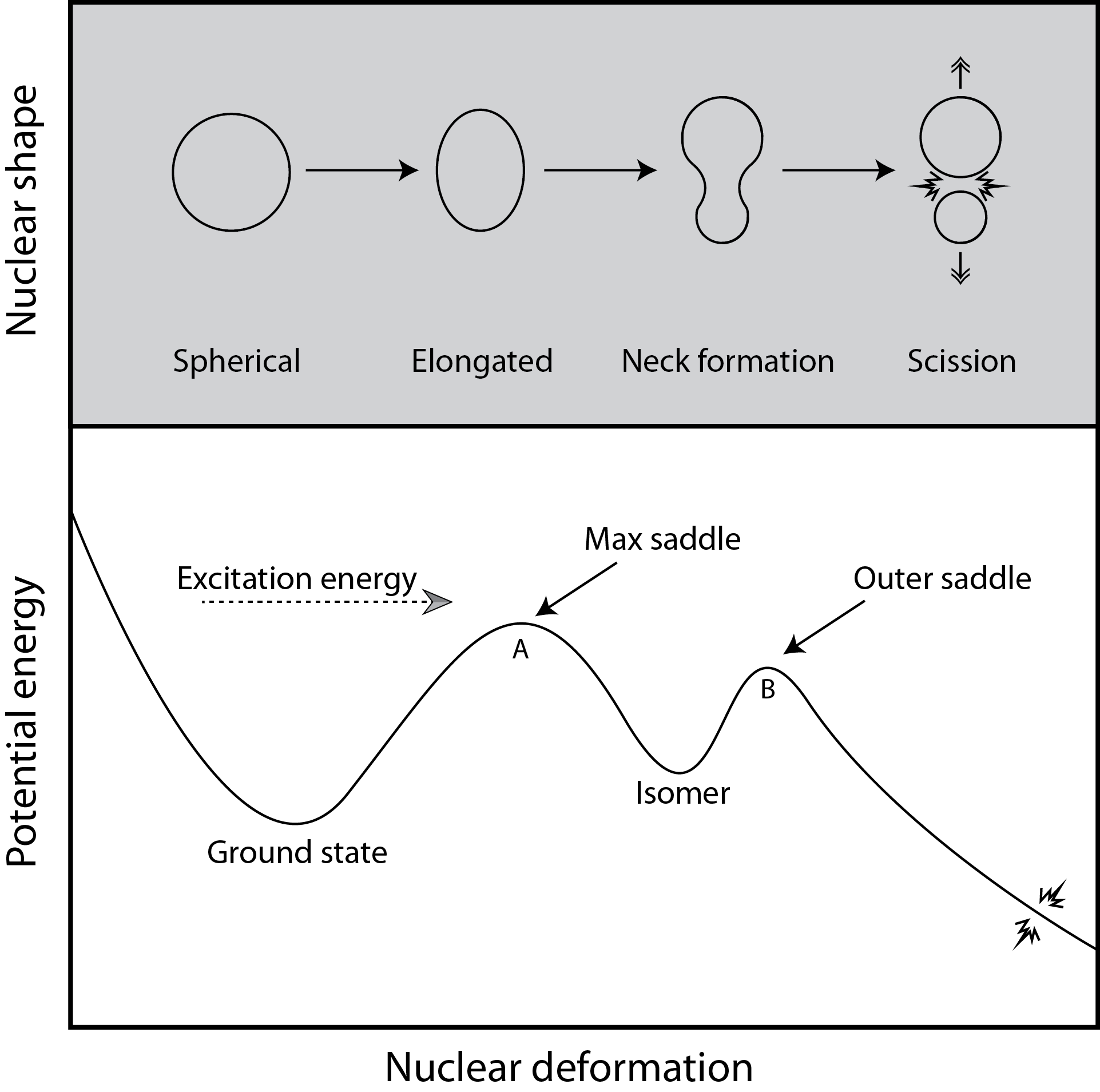
Follow progression of the nucleus from compact to highly elongated shapes
Fragment yield calculation (FRLDM)
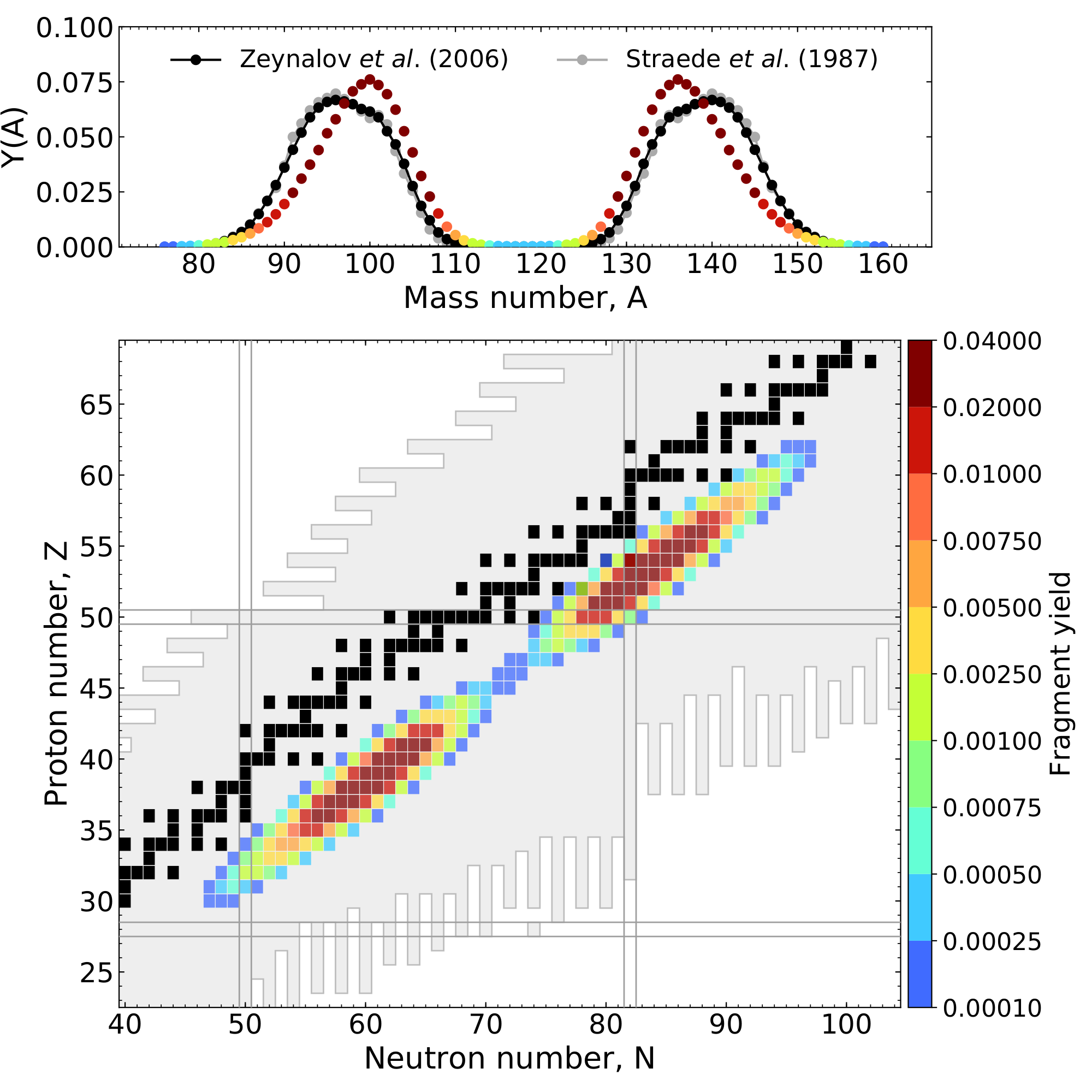
Ensemble of fission events leads to the cumulation of the yield curve ($^{235}$U + n$_{\rm{therm}}$)
Relies on geometric splitting argument for the scission configuration
Mass and charge yields both well reproduced
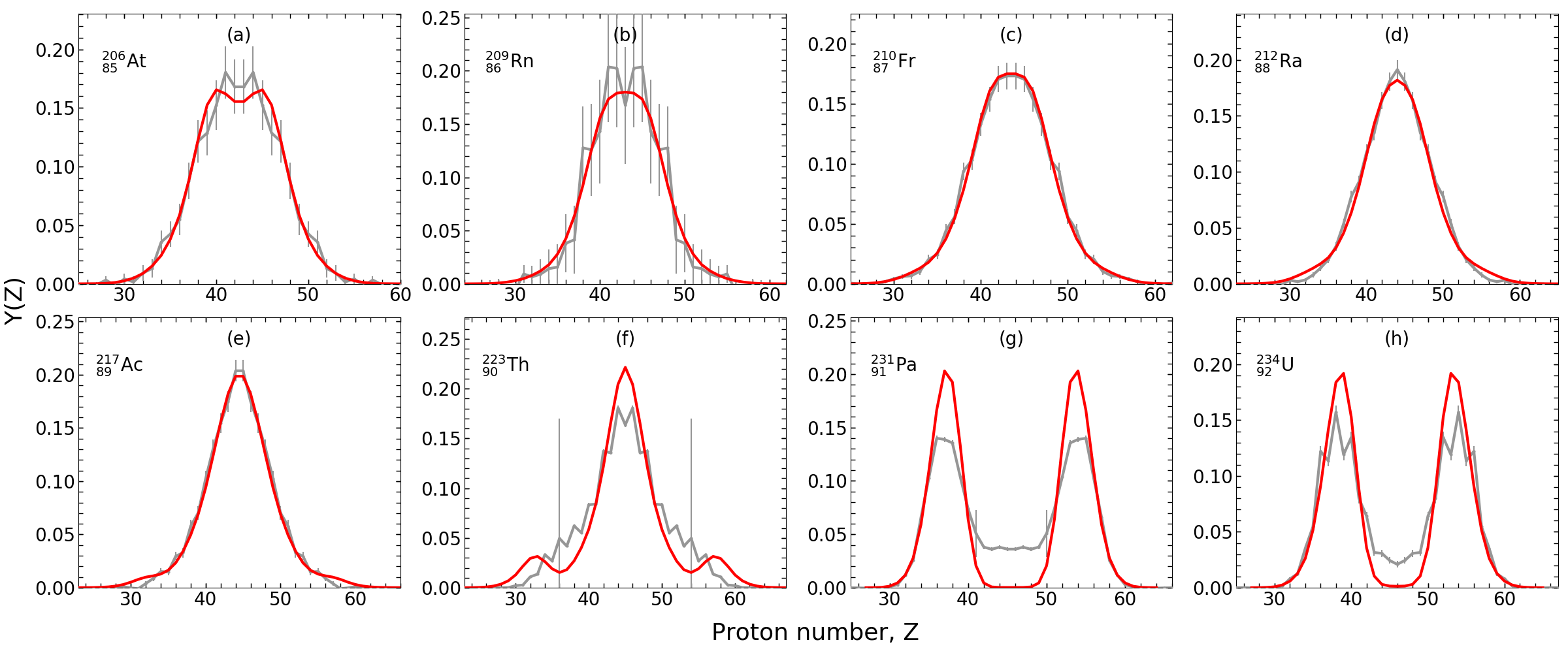
However! We could not simultaneously predict both...
Updates to our model (eFRLDM)
Higher resolution of Harmonic Oscillator basis
Improved treatment of the Strutinsky procedure
New Potential Energy Surfaces (PES) on a finer-grained, larger grid
New technique for obtaining fission yields in the limit of overdamped motion
Consequences
M. Verriere: first theoretical prediction of odd-even staggering using a particle number projection technique
We also obtain the charge polarization of the nascent fragment distributions in agreement with experiment
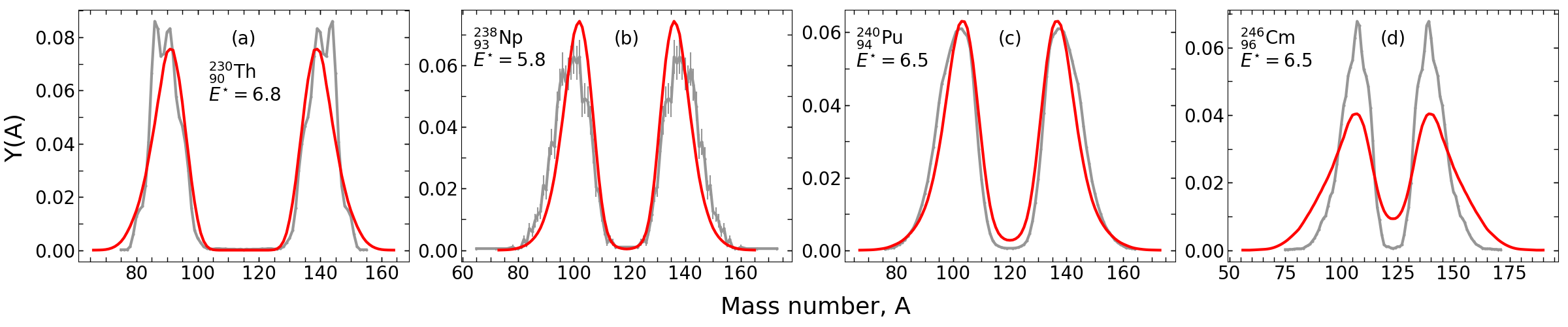
eFRLDM Results: $^{235}$U + n$_{\rm{therm}}$
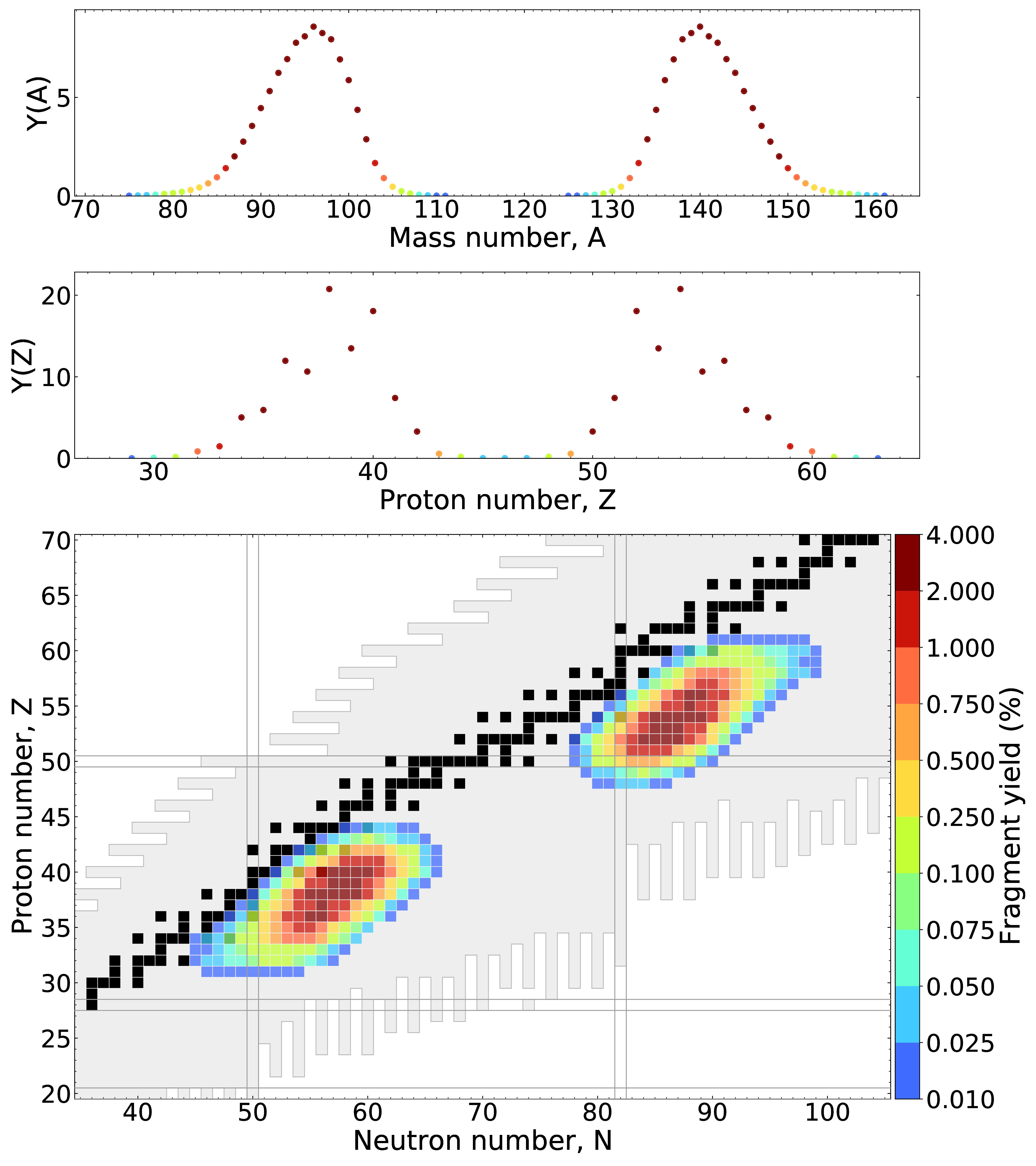
We can now describe Y(A), Y(Z) and Y(Z,A) simultaneously
eFRLDM Results: $^{235}$U + n$_{\rm{therm}}$
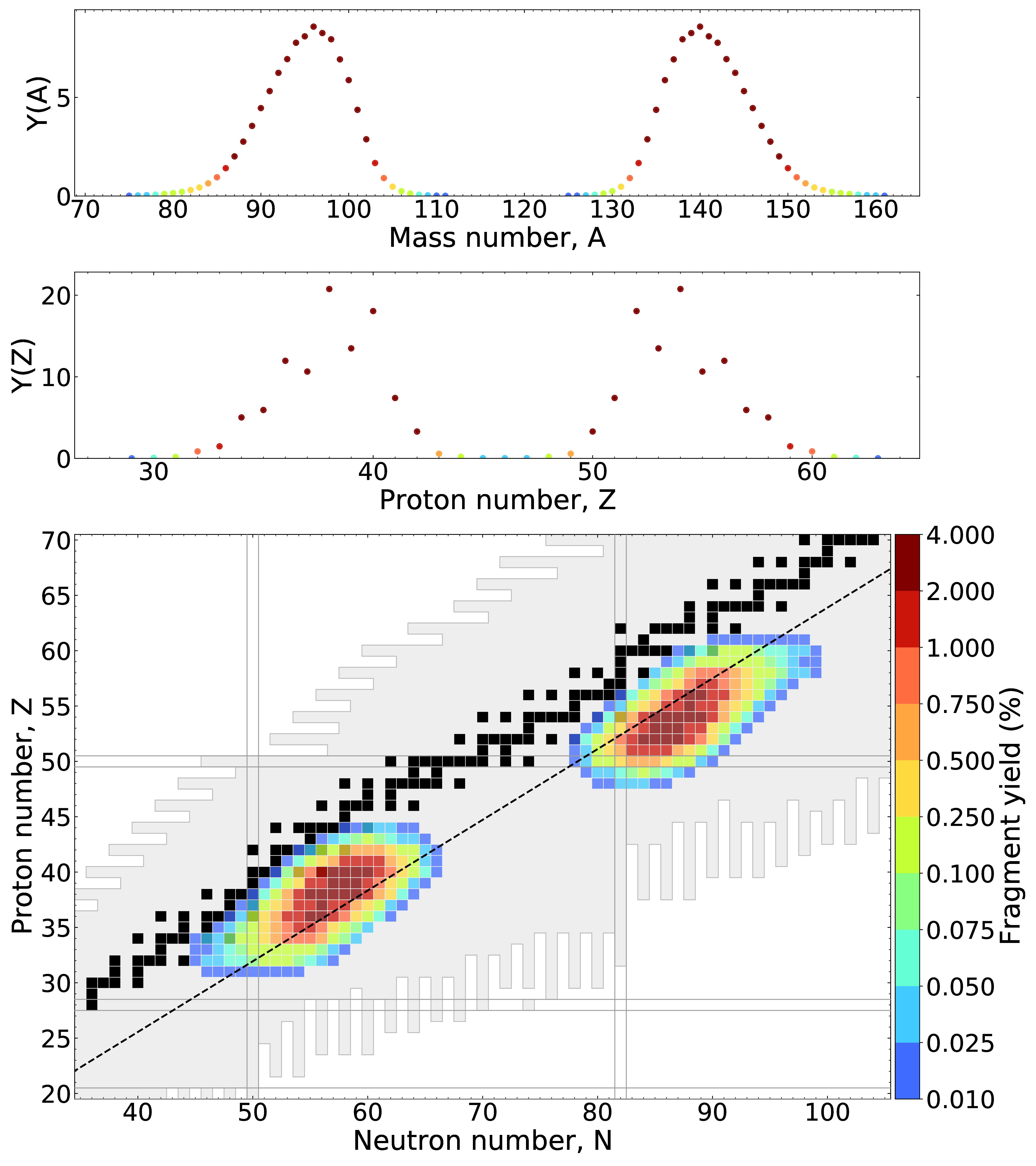
Fragment yields no longer follow unchanged charge distribution (UCD) assumption (Blacked dashed line)
eFRLDM Results: $^{235}$U + n$_{\rm{therm}}$
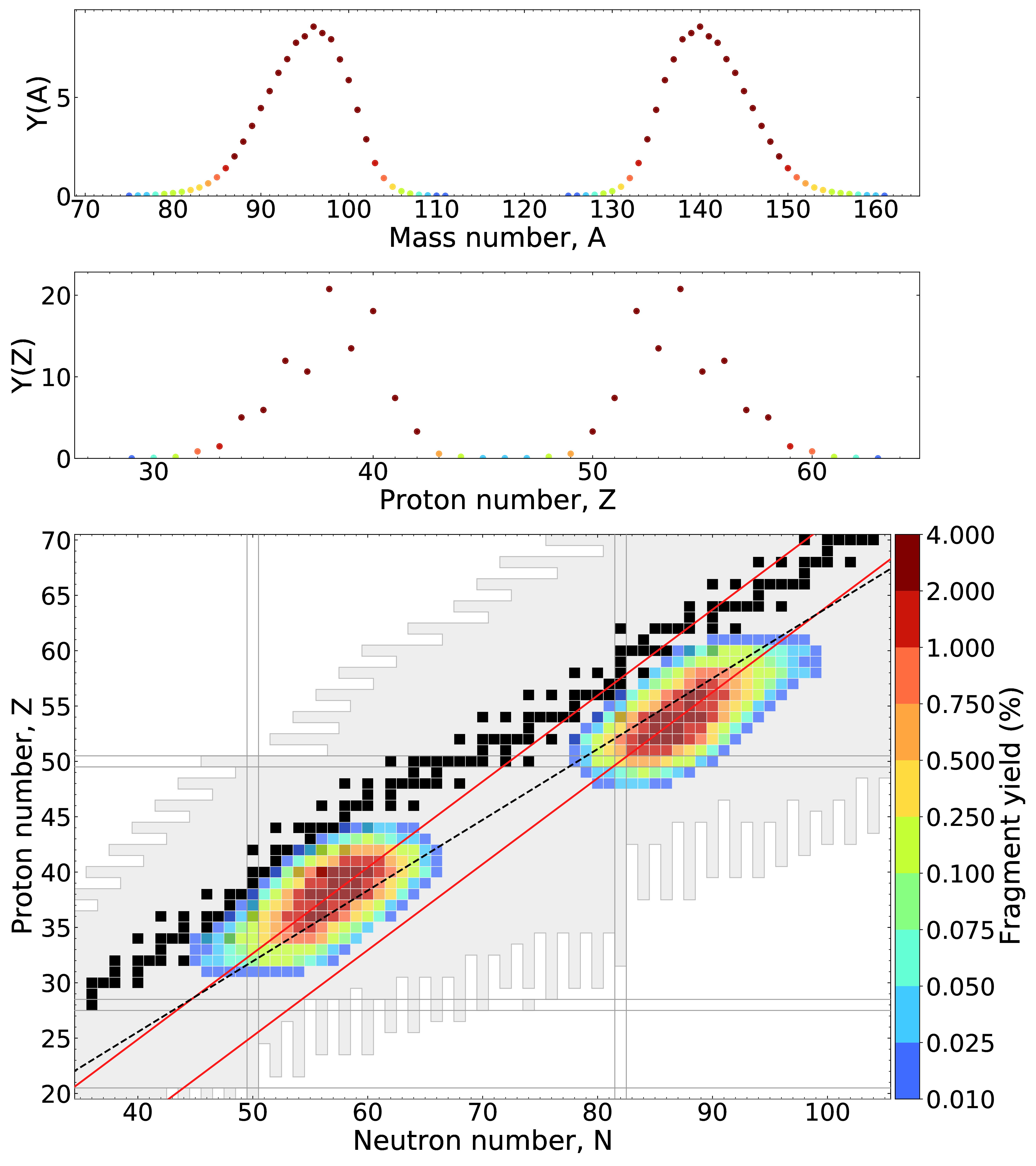
Charge polarization offset predicted and in agreement with experimental measurements (red lines)
Odd-even staggering in charge yields
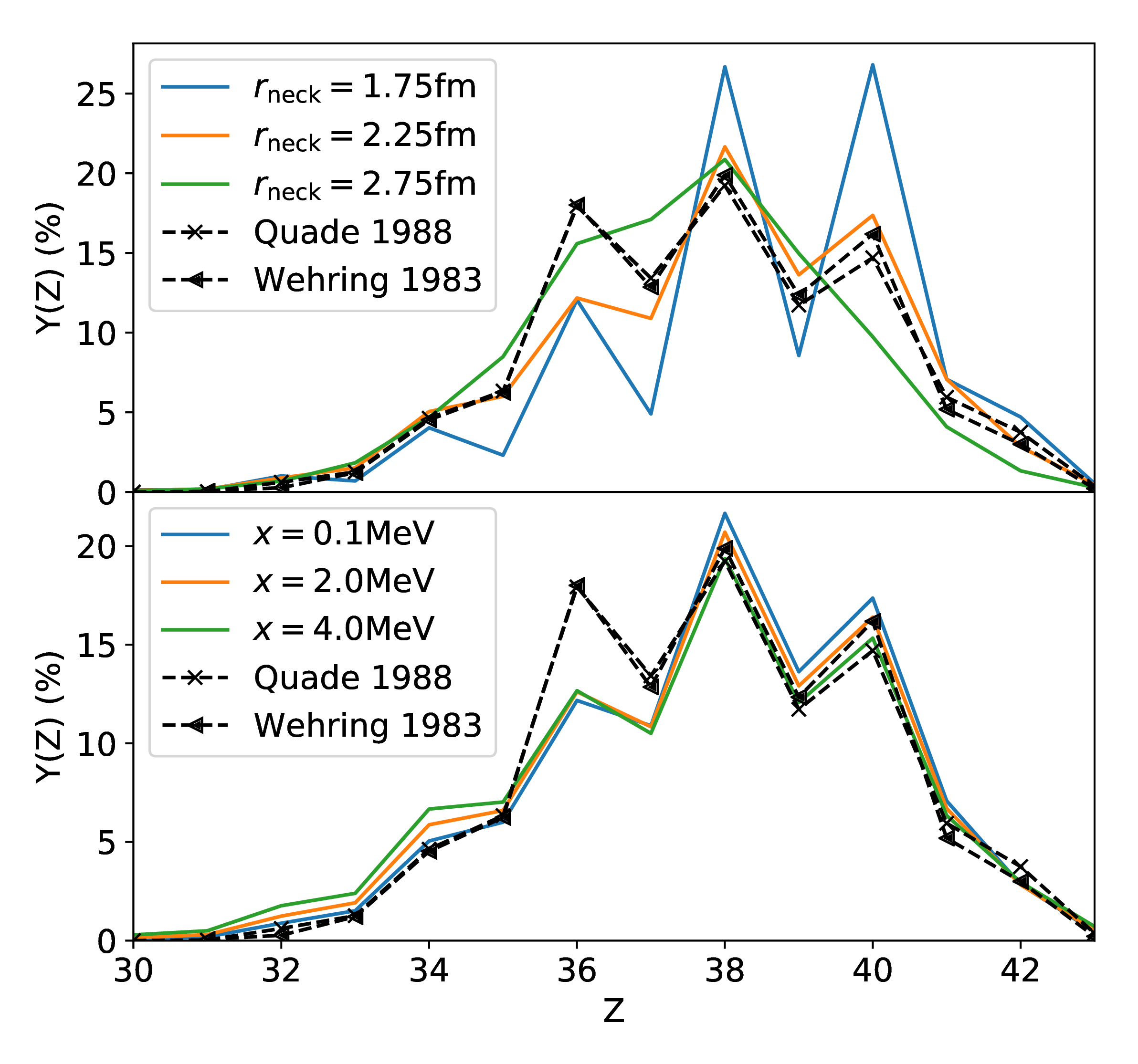
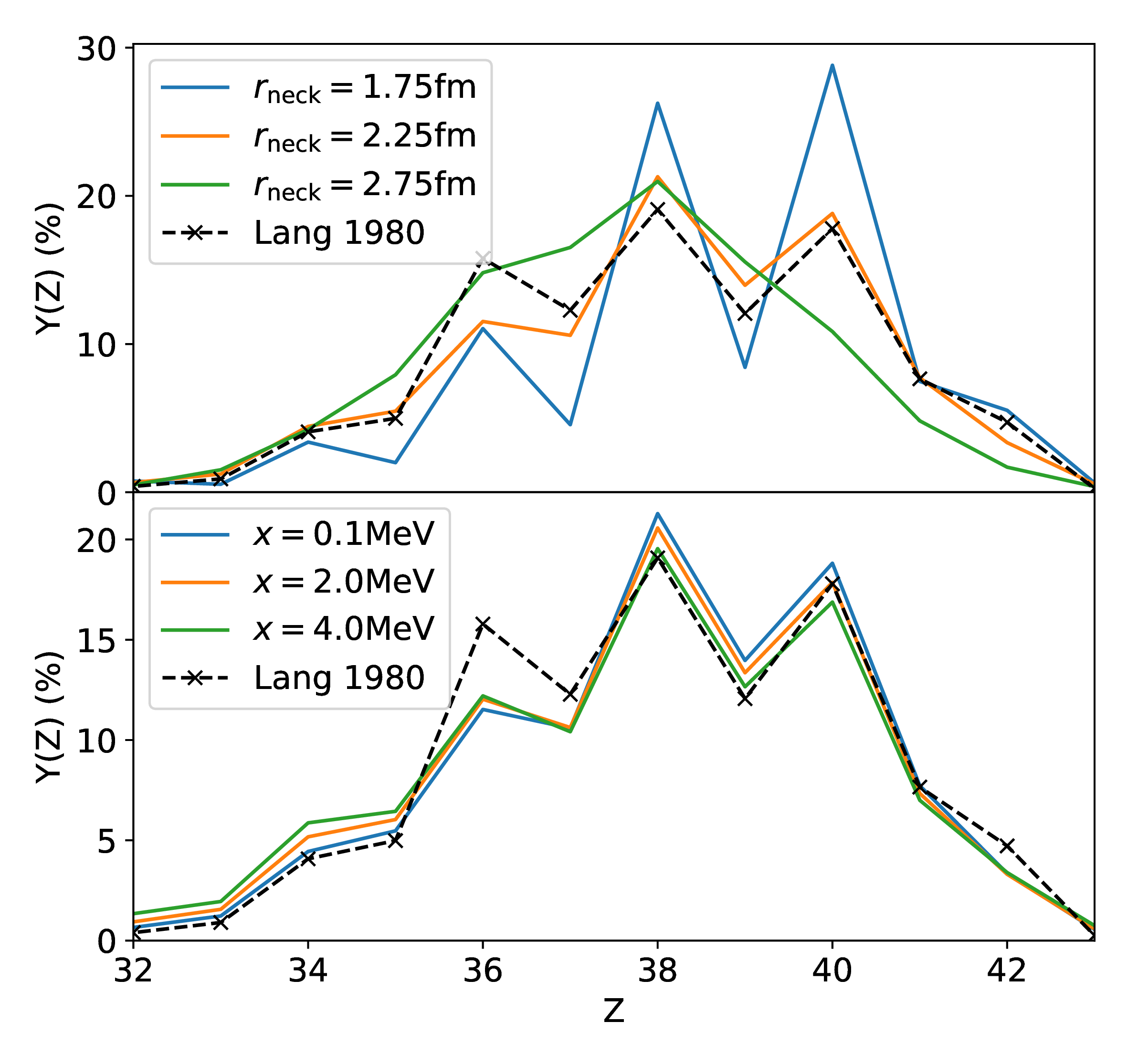
For the reactions ($^{233}$U + n$_{\rm{therm}}$) [left] and ($^{235}$U + n$_{\rm{therm}}$) [right]
First theoretical prediction of odd-even staggering using a particle number projection technique
Special thanks to
My collaborators
P. Jaffke, T. Kawano, J. Randrup, N. Schunck, T. Sprouse, I. Stetcu & M. Verriere
▣ Postdoc
Summary
Many modern applications require a deep understanding of fission
We have enhanced the FRLDM model to describe:
simultaneous fragment yields ▴ charge polarization ▴ odd-even staggering in charge yields
FRIB, etc. will help to constrain nuclear models, but the heaviest elements will remain relatively inaccessible
We therefore need to keep developing and studying theoretical models of nuclear physics, especially fission
Future upgrades to this type of fission modeling are in the works!
Results / Data / Papers @ MatthewMumpower.com