Fission fragment yield trends

        LA-UR-20-28896

Matthew Mumpower

Fall DNP

Sunday Nov. 1$^{st}$ 2020


Nuclear Data Team
Theoretical Division

Los Alamos National Laboratory Caveat

The submitted materials have been authored by an employee or employees of Triad National Security, LLC (Triad) under contract with the U.S. Department of Energy/National Nuclear Security Administration (DOE/NNSA).

Accordingly, the U.S. Government retains an irrevocable, nonexclusive, royaltyfree license to publish, translate, reproduce, use, or dispose of the published form of the work and to authorize others to do the same for U.S. Government purposes.

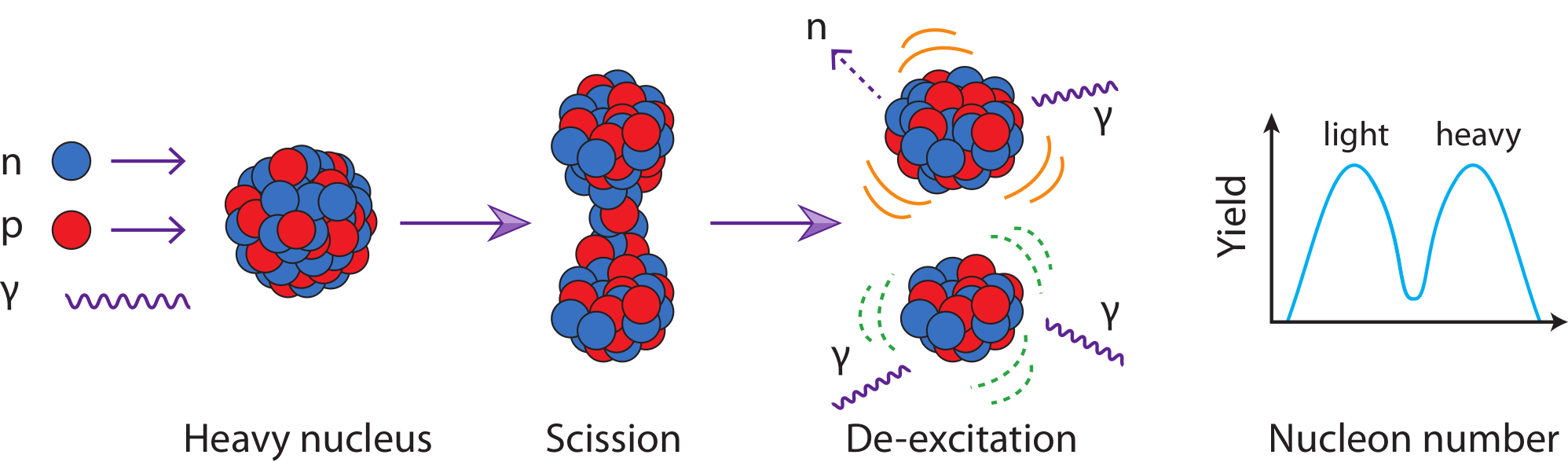
Why do we need fission yields?

Fission yields are needed for a variety of modern applications

Industrial applications: simulation of reactors, fuel cycles, waste management

Experiments: backgrounds, isotope production with radioactive ion beams (fragmentation)

Science applications: nucleosynthesis, light curve observations

Other Applications: national security, nonproliferation, nuclear forensics

Figure: Chi-Nu detector (left), Reactor cooling towers (middle), Neutron star merger (right)

The importance of understanding trends

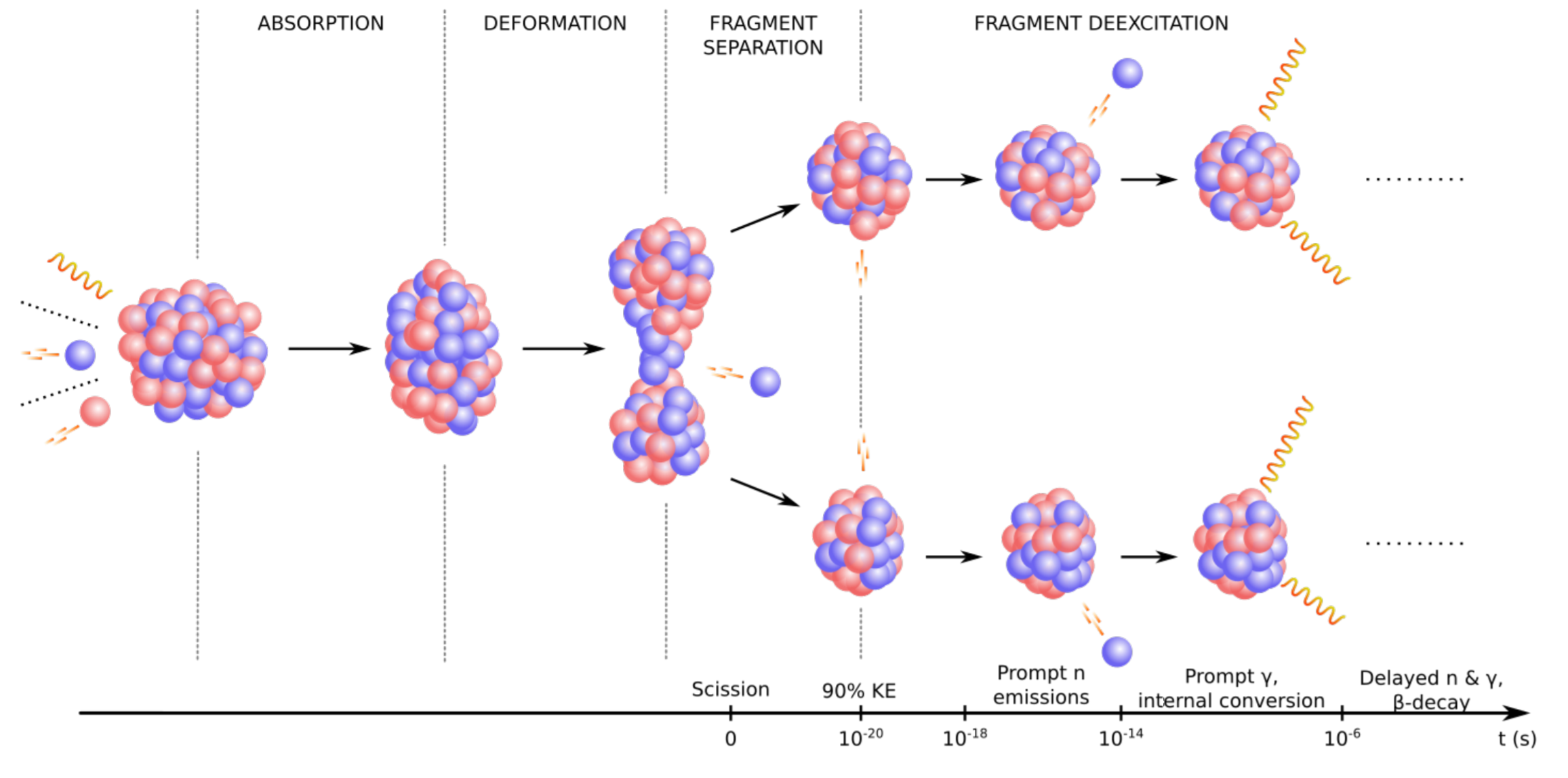
In particular, trends in yields across the chart of nuclides are very important

An understanding of trends can help us benchmark fission models

And help us to extrapolate or interpolate in regions where data is not available

We study trends in the context of the Finite-Range Liquid-Drop Model (FRLDM)

Möller et al. PRC (2009) • Möller et al. PRC (2015) • Figure by M. Mumpower

A basic picture of fission

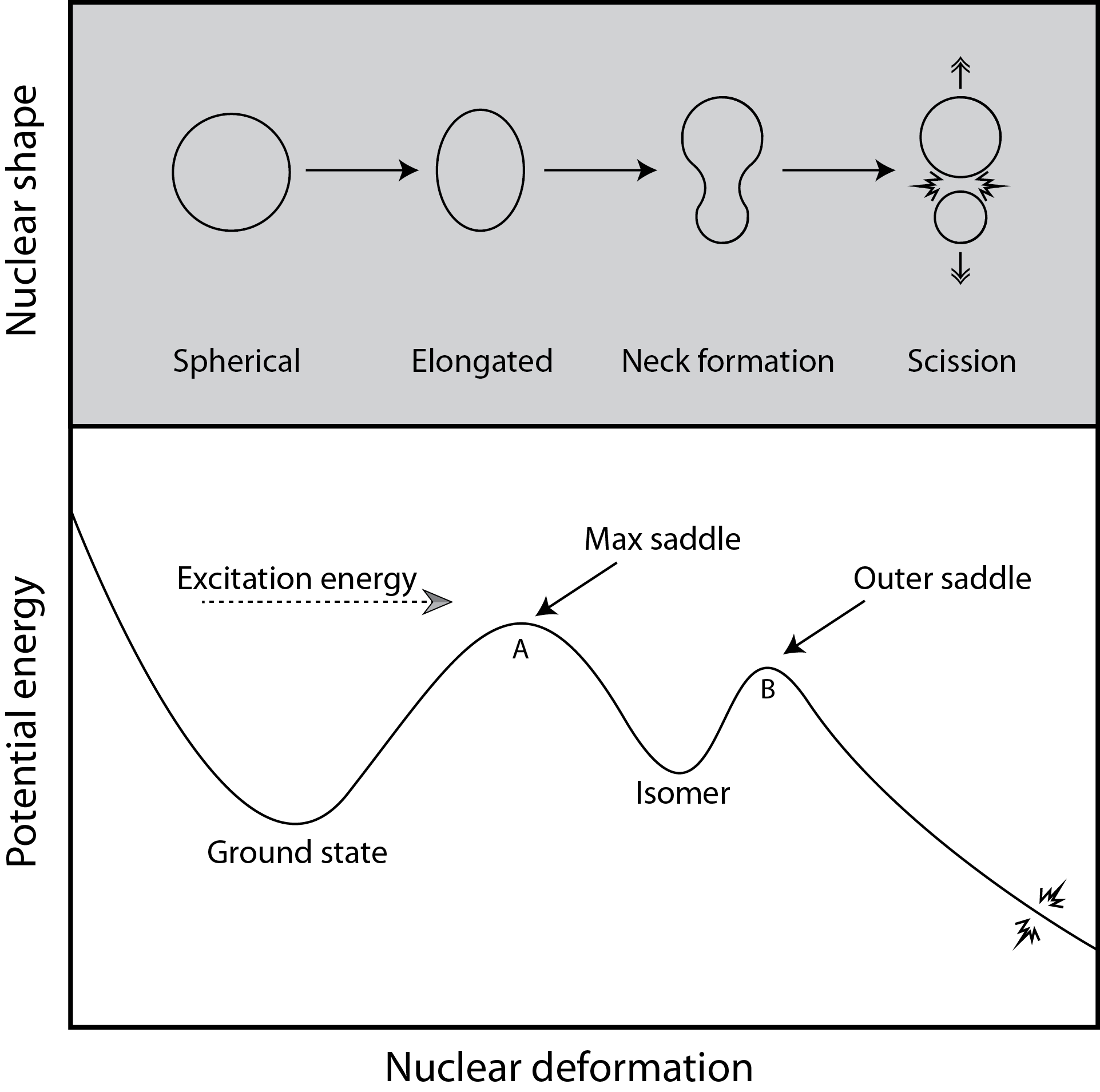
Follow progression of the nucleus from compact to highly elongated shapes

Randrup et al. PRL (2011) • Randrup et al. PRC (2011) • Randrup et al. PRC (2013) • Figure from Mumpower et al. PRC 101 054607 (2020)

Fragment yield calculation

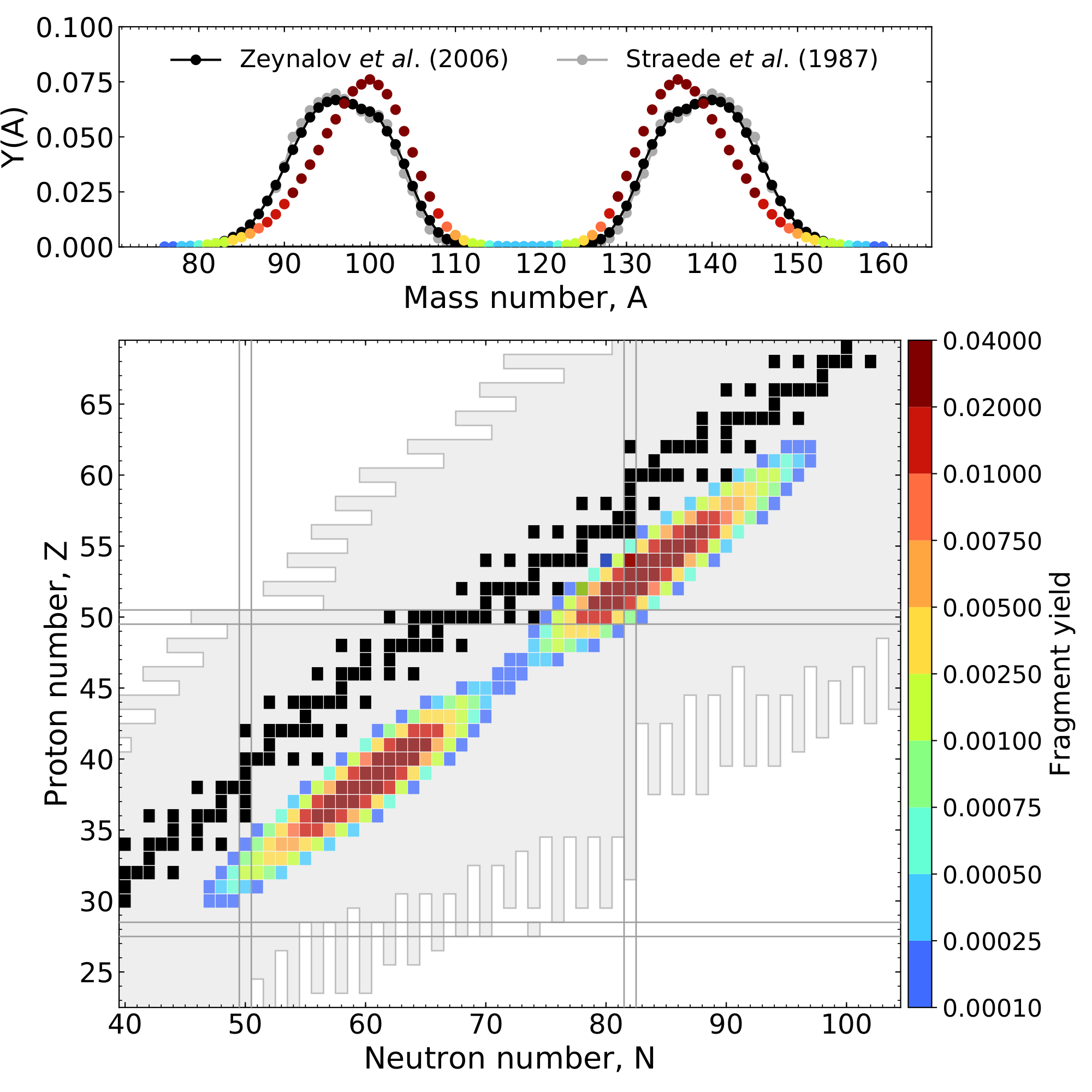
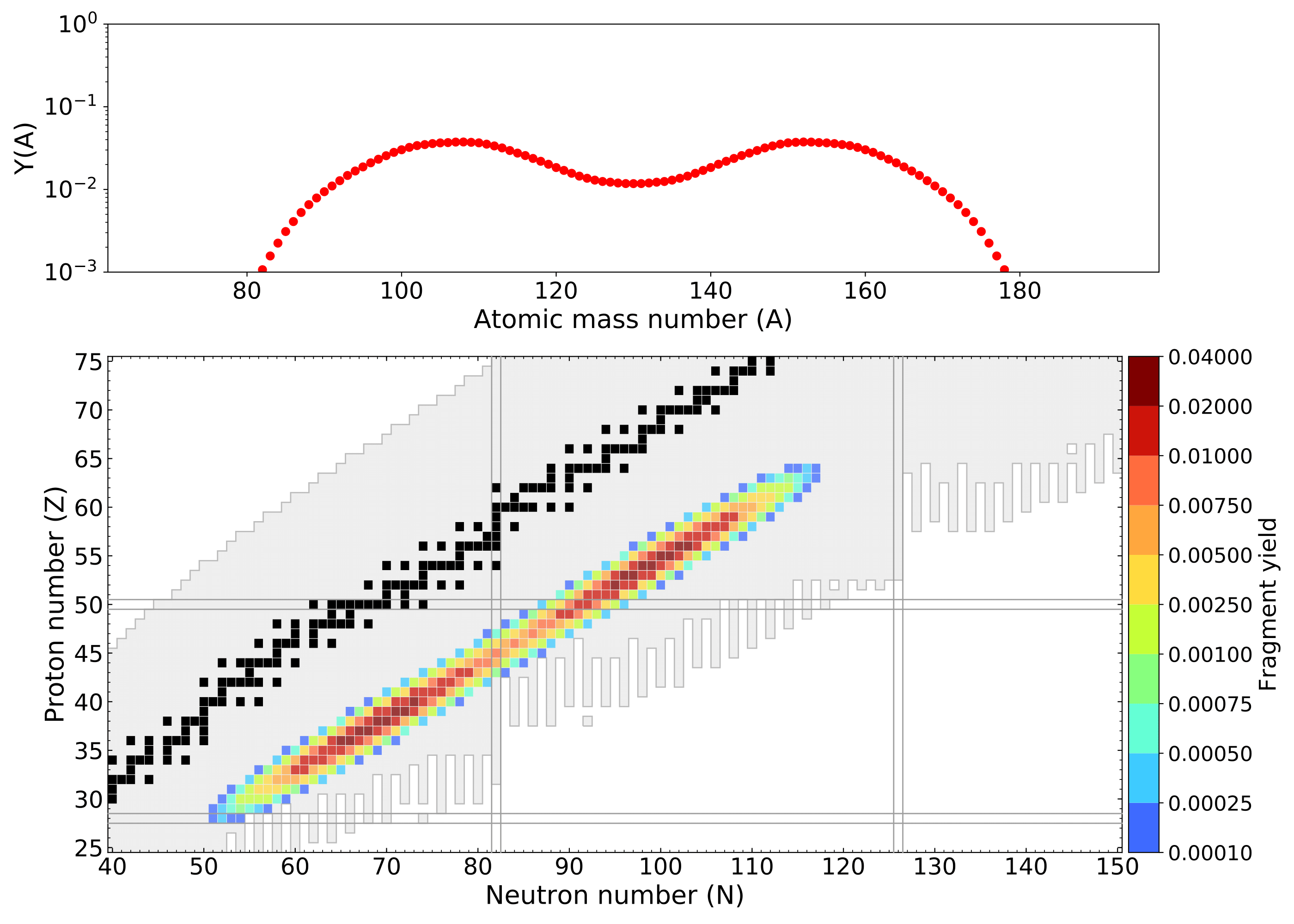
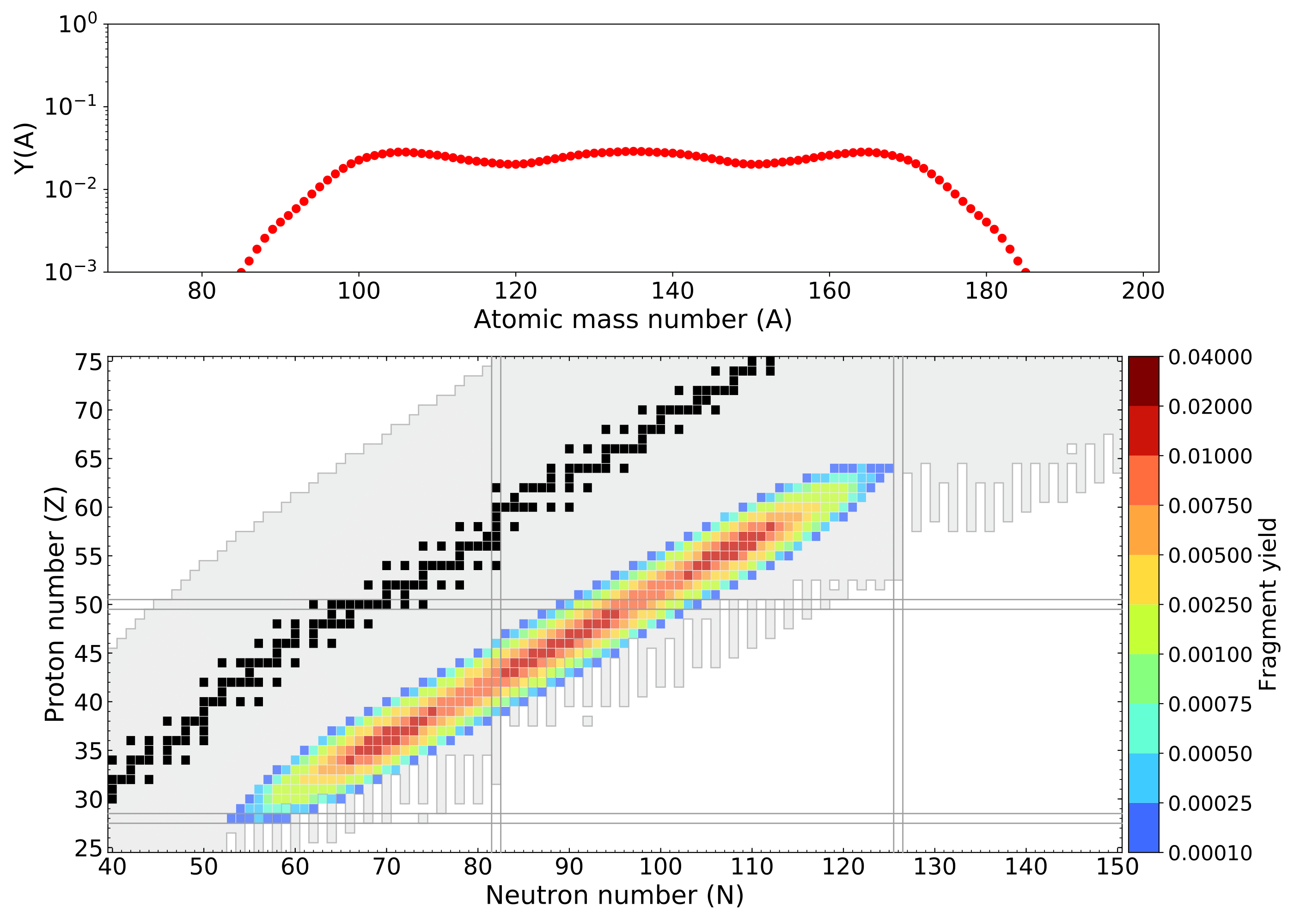
Ensemble of fission events leads to the cumulation of the yield curve ($^{235}$U + n$_{\rm{therm}}$)

Relies on geometric splitting argument for the scission configuration

Mumpower et al. PRC 101 054607 (2020)

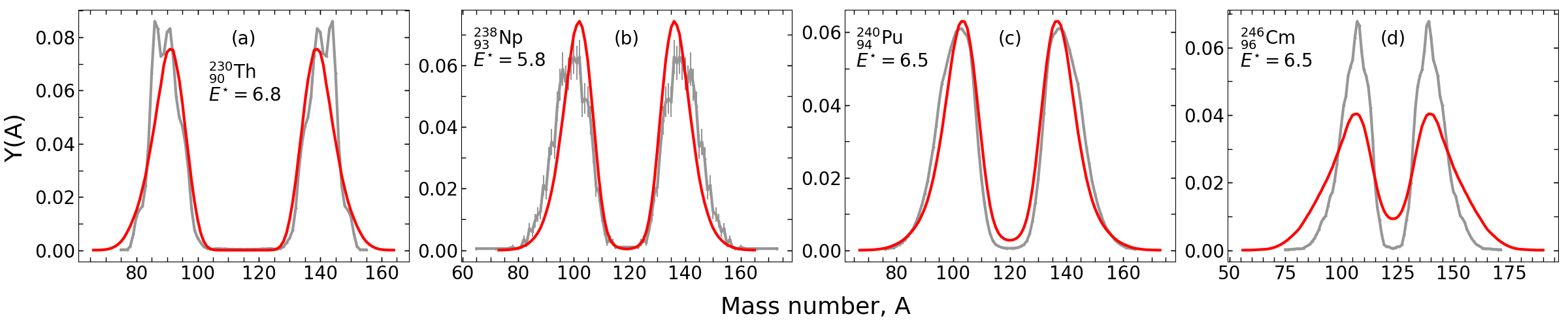
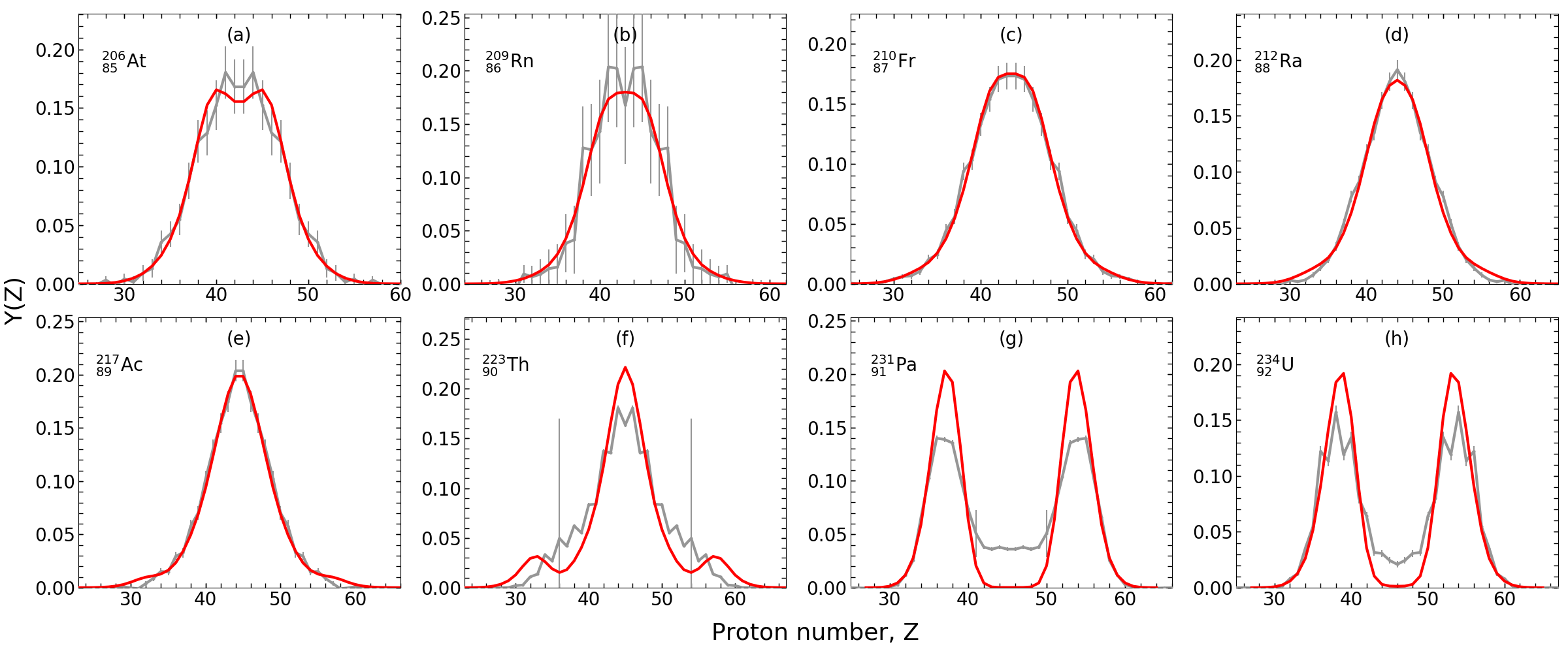
Mass and charge yields both well reproduced

Mumpower et al. PRC 101 054607 (2020)

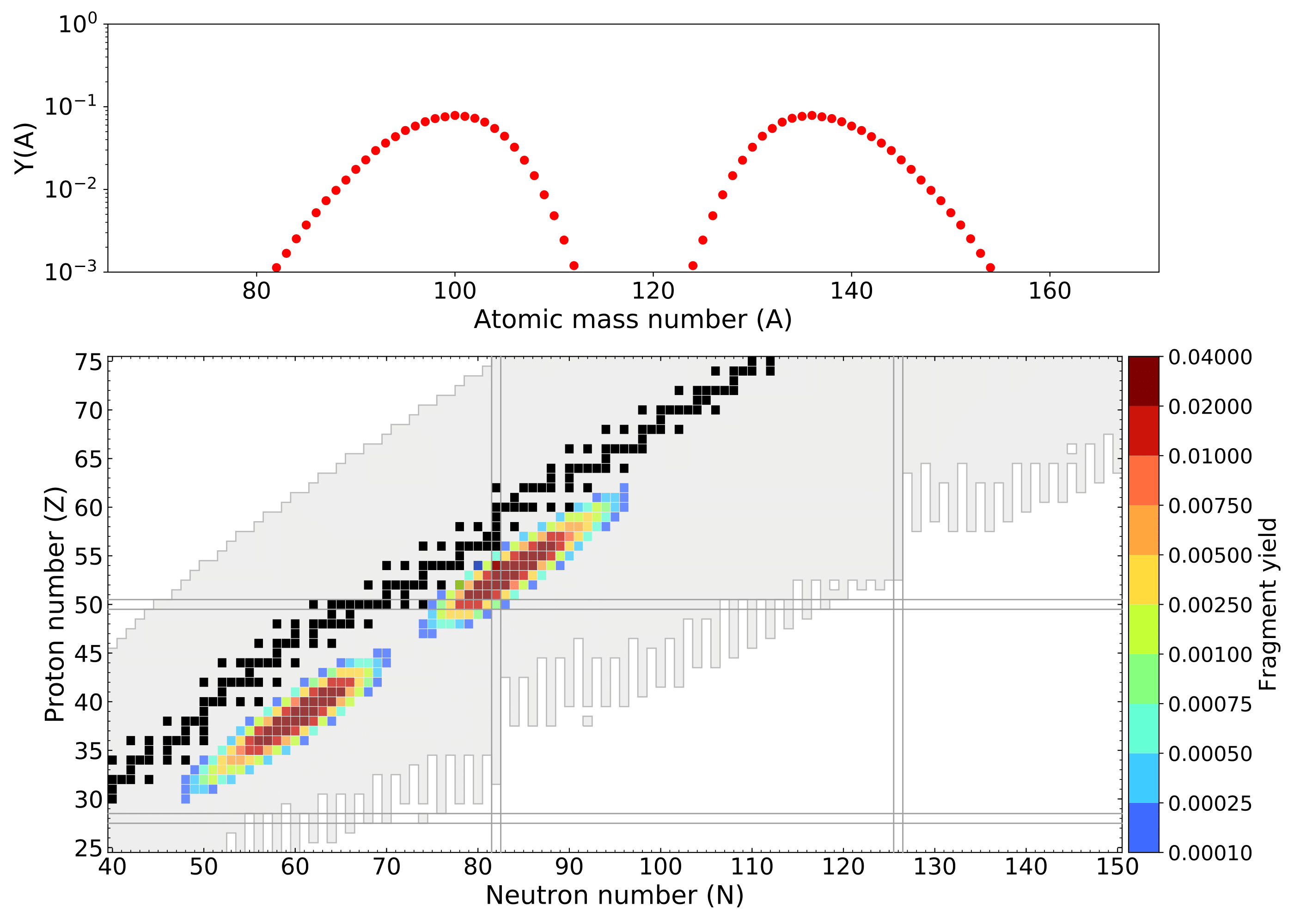
236-U Y(Z,A) yield

Mumpower et al. PRC 101 054607 (2020)

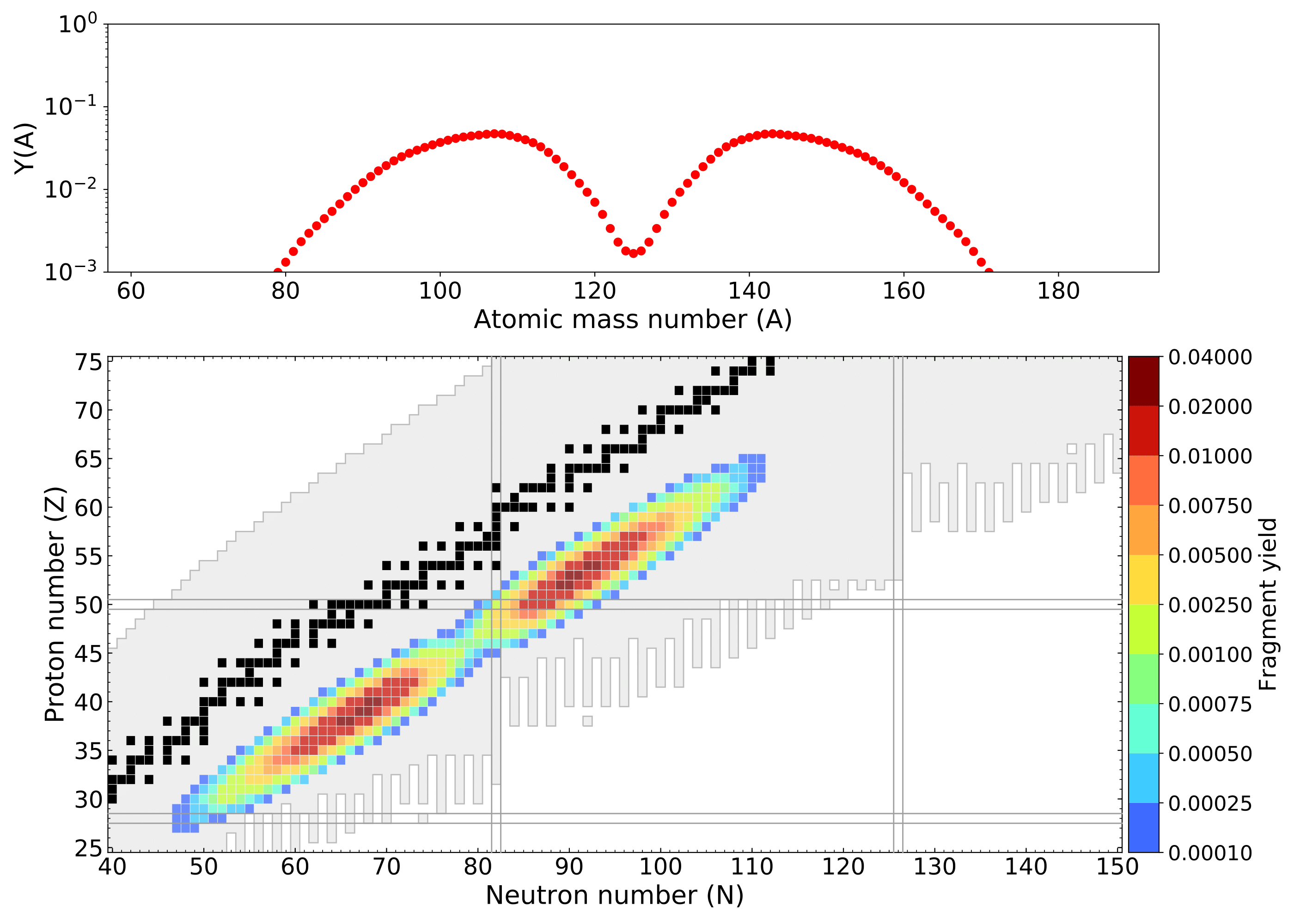
250-U Y(Z,A) yield

Mumpower et al. PRC 101 054607 (2020)

260-U Y(Z,A) yield

Mumpower et al. PRC 101 054607 (2020)

270-U Y(Z,A) yield

Mumpower et al. PRC 101 054607 (2020)

Number of Peaks

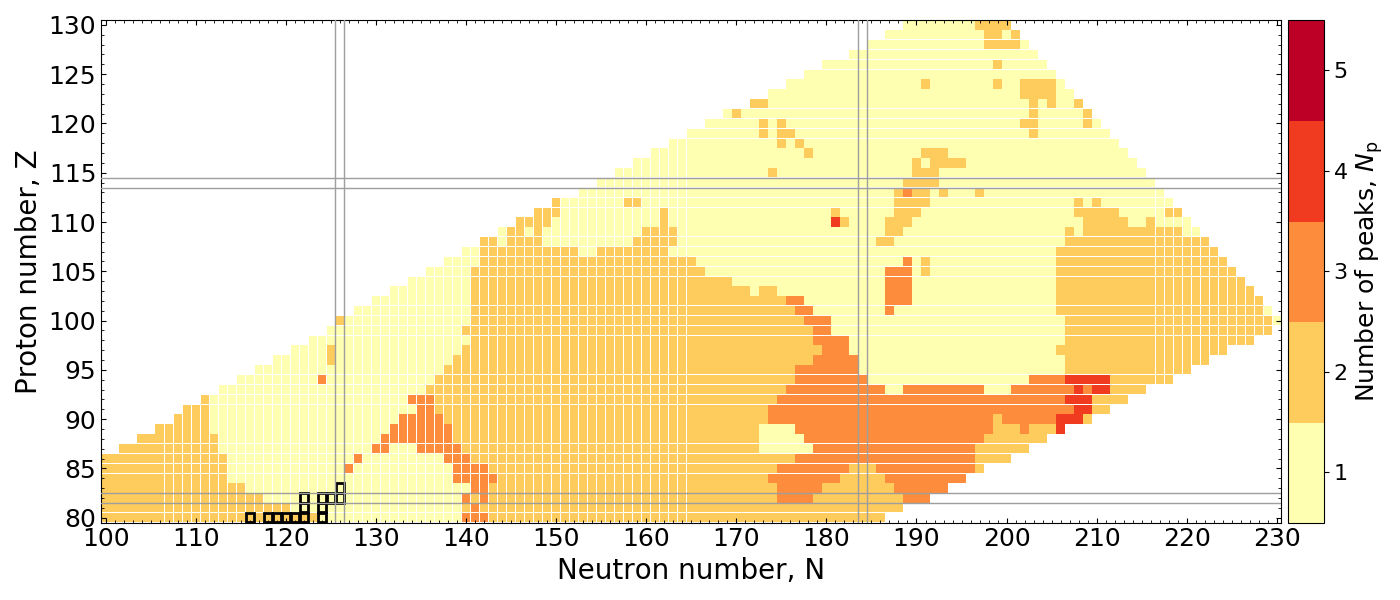
Count the number of peaks in the mass yield, $Y(A)$, distribution

Rather smooth variation in number of peaks across chart of nuclides.

$r$-process region: 2 or 3 peaks are the norm given our prediction of fission hot spots

Vassh et al. J. Phys. G (2019) • Mumpower et al. PRC 101 054607 (2020)

Measure of Asymmetry

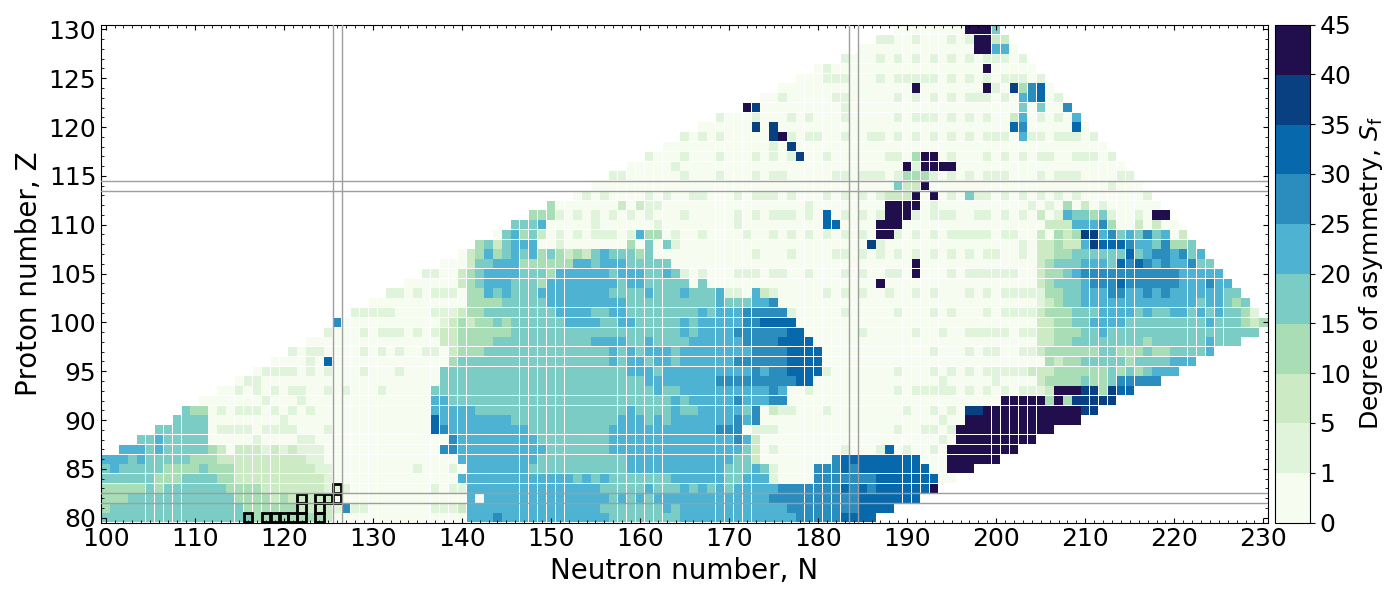
Measure the distance in $A$ between the maxima of $Y(A)$ and $Y(A_{\rm f}/2)$

Abrupt changes can be seen when the maxima shift from symmetric to asymmetric

Symmetric followed by asymmetric distributions can be expected in $r$-process simulations

Zhu et al. [arXiv:2010.03668] • Barnes et al. [arXiv:2010.11182] • Mumpower et al. PRC 101 054607 (2020)

Extent of Y(A) Distribution

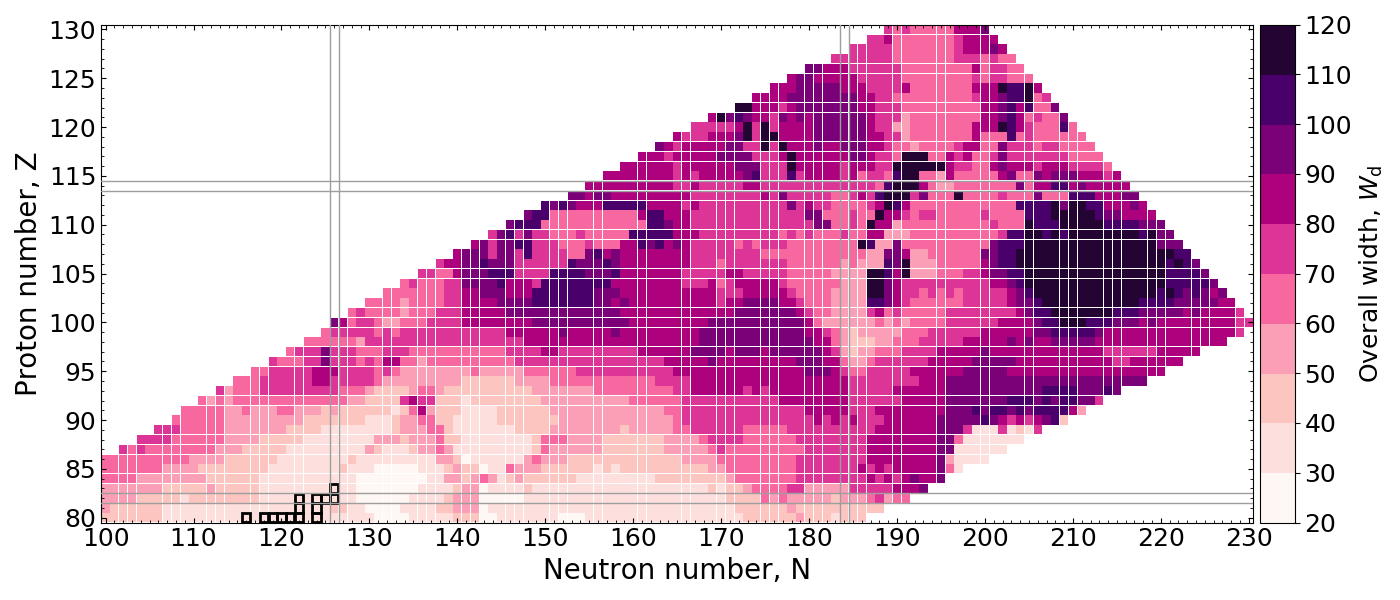
Measure the spread of the daughter products in $A$

Strong dependence can be seen with the fission system

Wiggles in the yield (number of peaks or asymmetry) don't matter if the distribution is wide!

Mumpower et al. PRC 101 054607 (2020)

Impact on $r$-process abundances

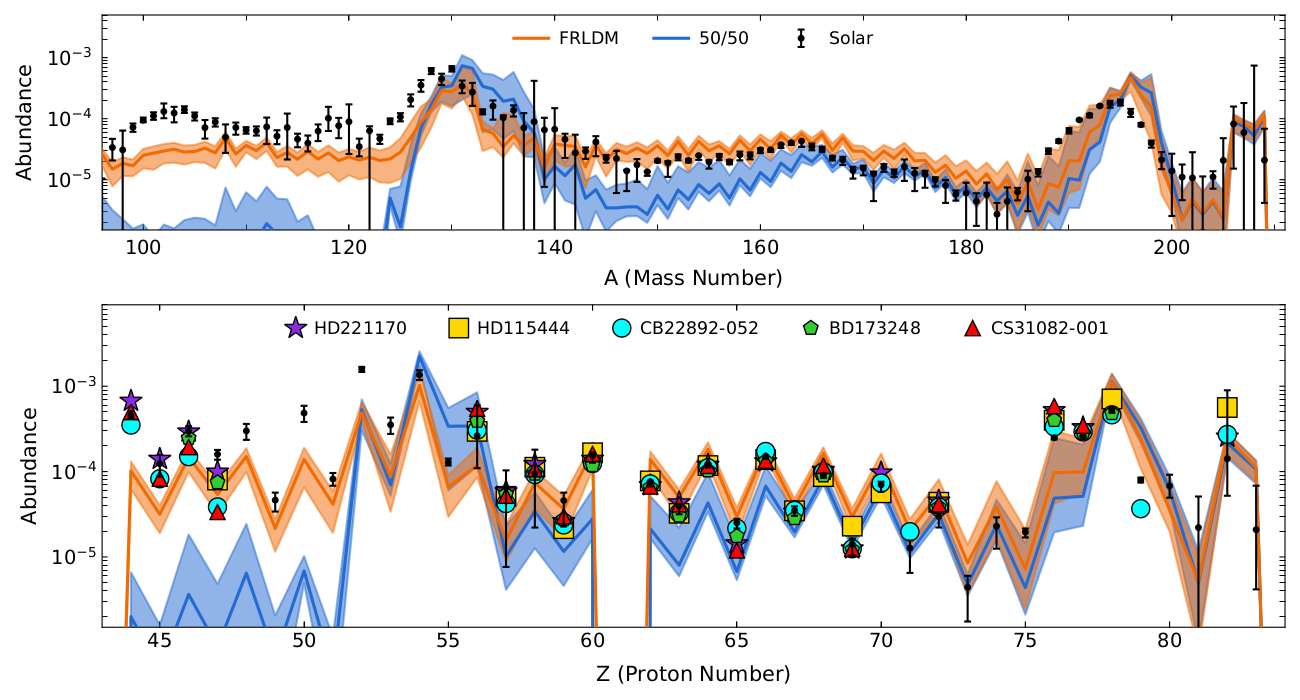
Abundance output using common old nuclear fission data and our new model predictions

Co-production of light nuclei from $Z\sim 45$ to the actinides (dynamical merger ejecta only!)

Universality may extend further down to lighter nuclei than commonly accepted in the literature

Vassh et al. ApJ 896 1 (2020)

Improvements to this approach

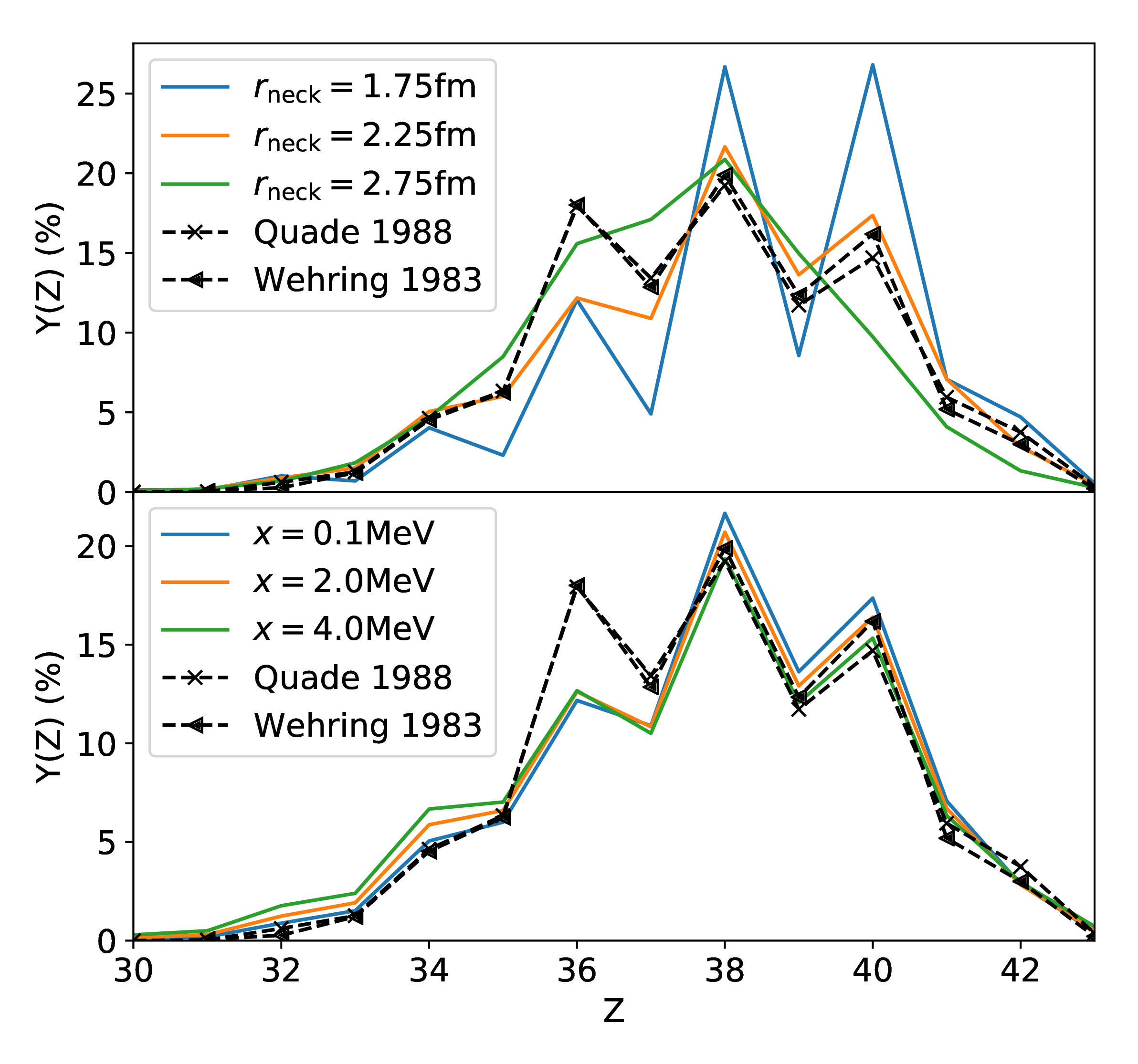
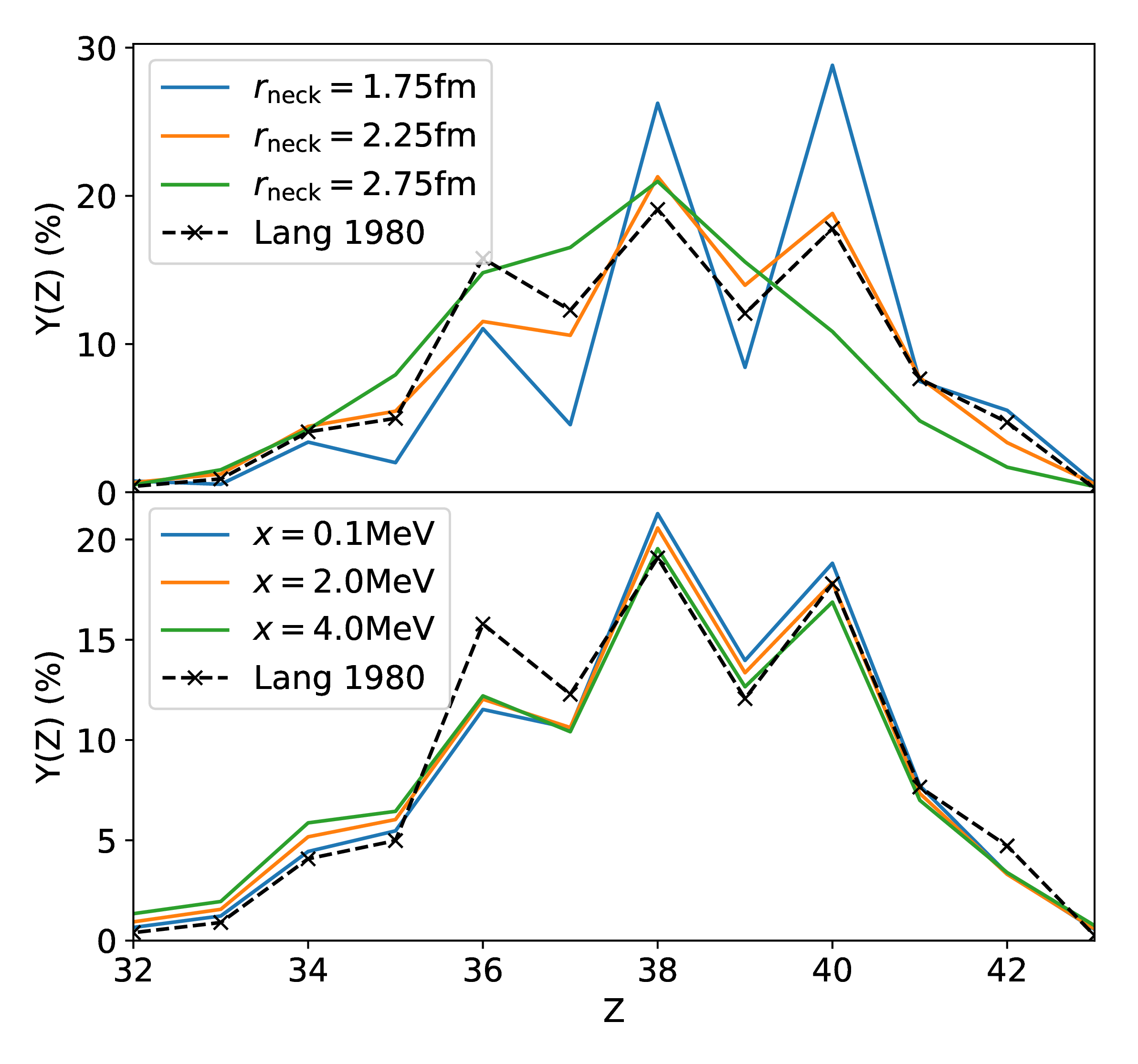
M. Verriere: first theoretical prediction of odd-even staggering using a particle number projection technique

We also obtain the charge polarization of the nascent fragment distributions in agreement with experiment

Verriere et al. PRC 100 024612 (2019) • Verriere & Mumpower [arXiv:2008.06639] (2020)

Special thanks to

My collaborators

J. Barnes, E. Holmbeck, P. Jaffke, T. Kawano, K. Lund, G. C. McLaughlin, P. Möller, J. Randrup, N. Schunck, D. Shaw, T. Sprouse, R. Surman, N. Vassh, M. Verriere, R. Vogt & Y. Zhu

▣ Student   ▣ Postdoc   ▣   FIRE PI


FIRE Collaboration
Fission In R-process Elements

Summary

Many modern applications require a deep understanding of fission

In particular, the astrophysical formation of the heavy elements in the $r$-process

Recent calculations give insight into:

fragment yield trends ▴ Production / destruction of heaviest elements ▴ odd-even staggering in charge yields

FRIB, etc. will help to constrain nuclear models, but the heaviest elements will remain relatively inaccessible

We therefore need to keep developing and studying theoretical models of nuclear physics, especially fission

Nuclear modeling is absolutely crucial if we want to prove definitively that heavy elements such as the actinides were made in an astrophysical event

Results / Data / Papers @ MatthewMumpower.com